このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
ドモルガンの法則
この式は公式みたいなものがあるんですか、それともベン図を書いてわかるものなのですか。よろしくお願いします。
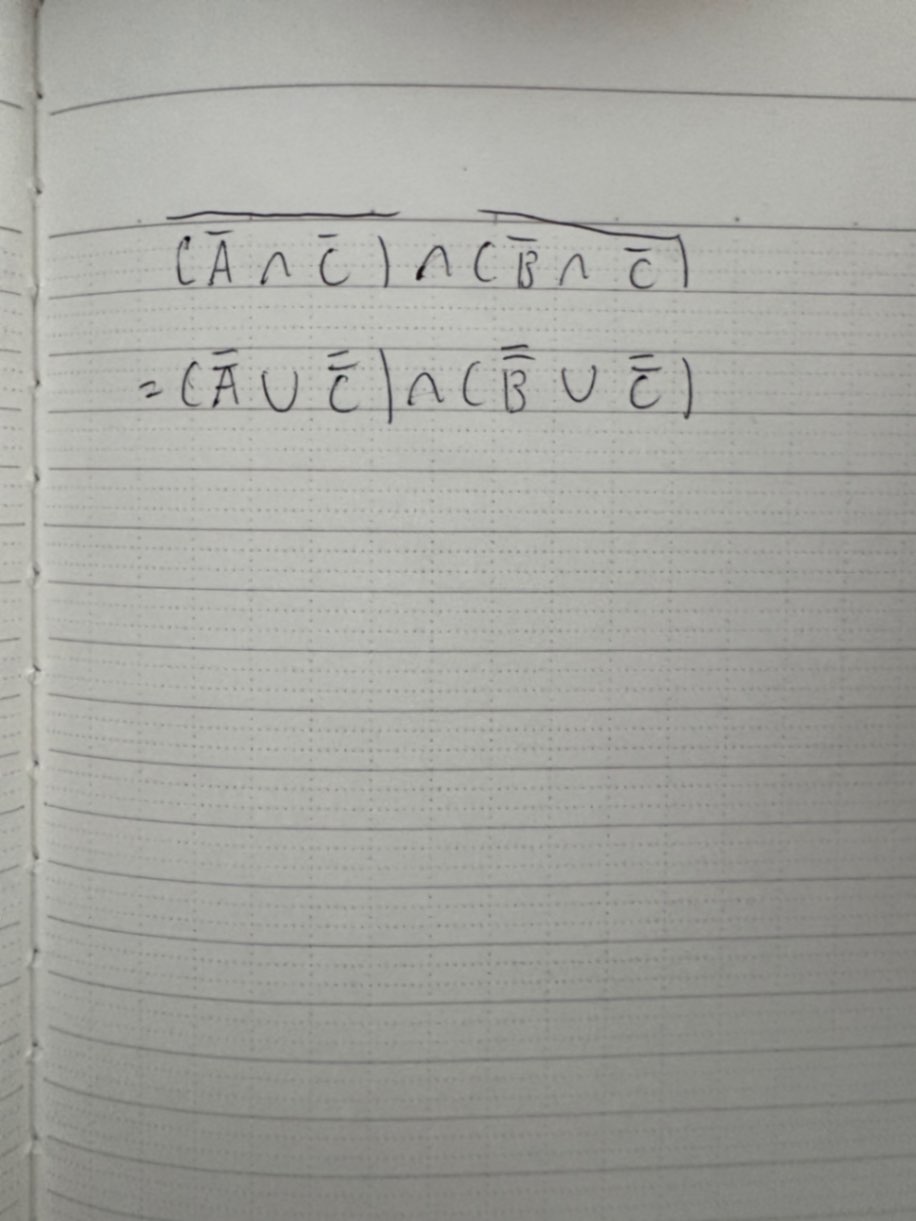
回答
R さん、こんばんは。
このページの質問はどこのことを指して言っているのかわかりません。
1行目から2行目に行くところ?
ド・モルガンの法則については理解できてる?
その法則自体はベン図を書けば確かめられますので、ベン図で理解しておけばいいです。
でも、それを利用して集合の式を変形していくときはベン図では無理で、ド・モルガンの法則をどのように当てはめるかに神経を集中させますよ!
前の質問の問題をかみ砕いて書いてみますので、まずそれを読んでください。
$\overline{(\overline{A}\cap \overline{C})\cup (\overline{B}\cap \overline{C})}$
$\overline{A}\cap \overline{C}=P,\overline{B}\cap \overline{C}=Q$ と書き換えれば
$\overline{P\cup Q}$ だから、ド・モルガンの法則により
$=\overline{P}\cap \overline{Q}$ となるので、元に戻せば
$\overline{(\overline{A}\cap \overline{C})}\cap \overline{(\overline{B}\cap \overline{C})}$ ……① となる。
次に、$\overline{A}=S,\overline{B}=T,\overline{C}=U$ と書き換えれば
ド・モルガンの法則を適用して
$\overline{(\overline{A}\cap \overline{C})}=\overline{S\cap U}=\overline{S}\cup \overline{U}=\overline{\overline{A}}\cup \overline{\overline{C}}$
$\overline{(\overline{B}\cap \overline{C})}=\overline{T\cap U}=\overline{T}\cup \overline{U}=\overline{\overline{B}}\cup \overline{\overline{C}}$
補集合の補集合は元の集合だから、それぞれ $(A\cup C), (B\cup C)$ となり、
①=$(A\cup C)\cap (B\cup C)$
この式では後ろ側の $\cup C$ が共通しているので、分配法則の逆で
$=(A\cap B)\cup C$
となります。
問題文がはっきり見えないのでどこまでやればいいのかわかりませんが、図示するならここまで来れば書けるでしょう。
これで大丈夫ですか?
納得できないところがあれば言ってください。コメント欄になにか返事を書いてください。
わかりました。ありがとうございます!
これで大丈夫だったのですか?それならよかったです。またどうぞ!