このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
明治大学 経営学部 数学 過去問 大問2
写真にある(3)(4)がわからないです。
内接円の半径が3/2で外接円の半径が7であるのは分かりました。内分などを使って解こうとしましたができませんでした。

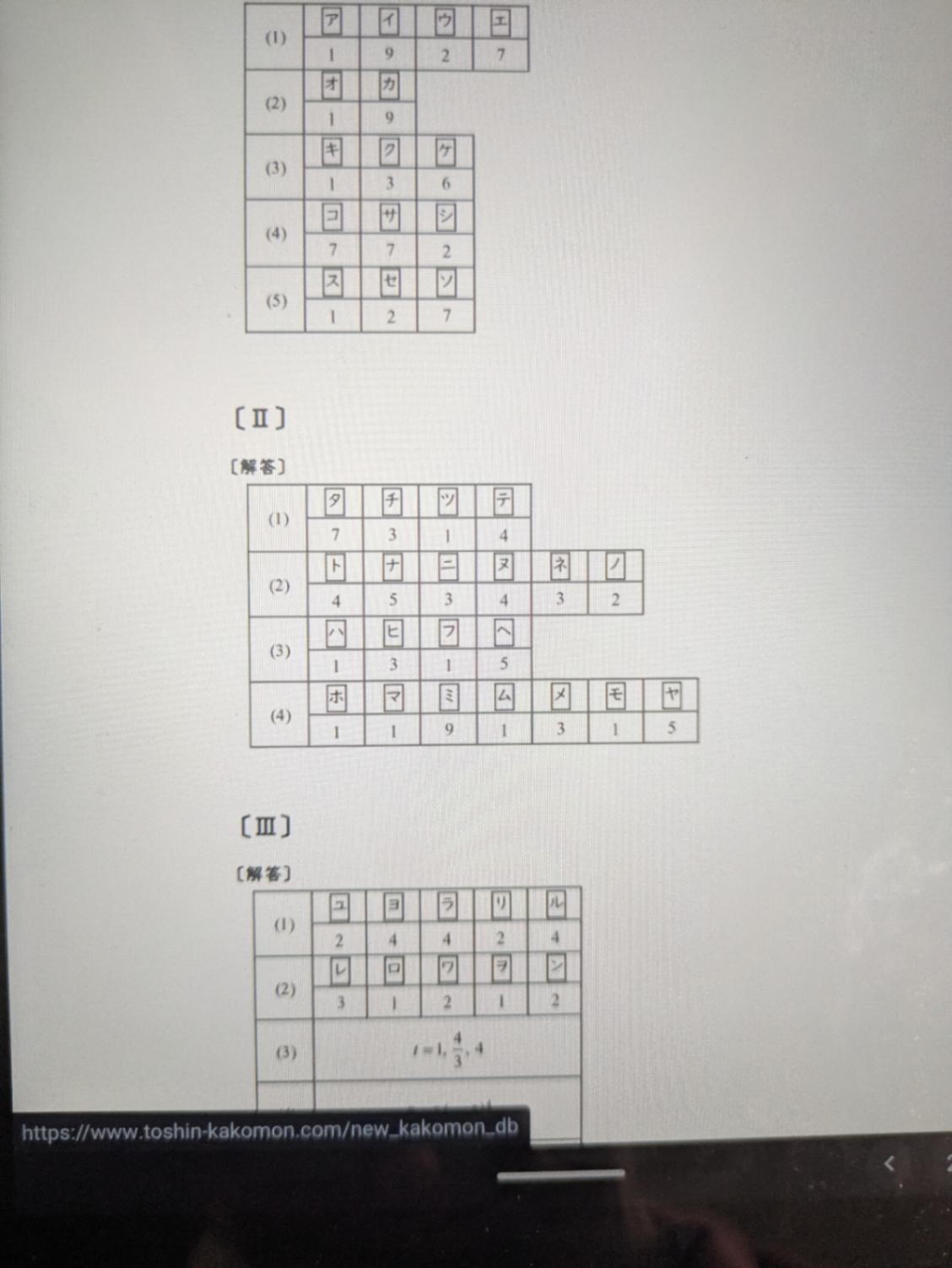
回答
長谷川 健介 さん、こんばんは。はじめてのかたですね。よろしく。
もう閉店時間なので、半分だけ。
内心 I は∠Aの2等分線上にあります。
角の2等分線の方向を表すベクトルは作れますか?
$\overrightarrow{a}$ と $\overrightarrow{b}$ が作る角の2等分線の方向は
$\dfrac{\overrightarrow{a}}{|\overrightarrow{a}|}+\dfrac{\overrightarrow{b}}{|\overrightarrow{b}|}$
で表わされるというのは分かりますか?2つのベクトルそれぞれの方向の単位ベクトルを作って足すと、2つのベクトルがなす角の2等分線上になりますよ!
これを使います。
$\overrightarrow{AI}=k\left(\dfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}+\dfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\right)$
と書けて、しかもその長さが3/2なのですね。つまり上の式の右辺の自分自身との内積が9/4だ、という式を作ると、そこからkが求まり、
$s=\dfrac{k}{3\sqrt{3}},t=\dfrac{k}{5\sqrt{3}}$ となります。
この方針でやってみてください。
ここではなるべくヒントや方針を書くだけで、あとは自分でやってみた方がいいと思うのです。
もう遅いので閉店します。後半は明日になりますが、ゴカンベンを!
ここでは会話型を目指しています。とりあえずこれを読んでやってみたら、できたとか、分かったとか、この辺がわからないので説明してくれとか、下のコメント欄になにか返事を書いてください。よろしく。
回答ありがとうございます。 その方針で解いてみて解くことが出来ました。
「明日になります」などと書いておいて遅れてしまい、申し訳ない! 後半の外心についても解けたのですか? 後半も回答した方がいいですか、もう大丈夫ですか?