このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
Cosθ
写真の問題についてなのですが、
この様に考えてはいけないのは、三角形の右下に90°を作れないからでしょうか?
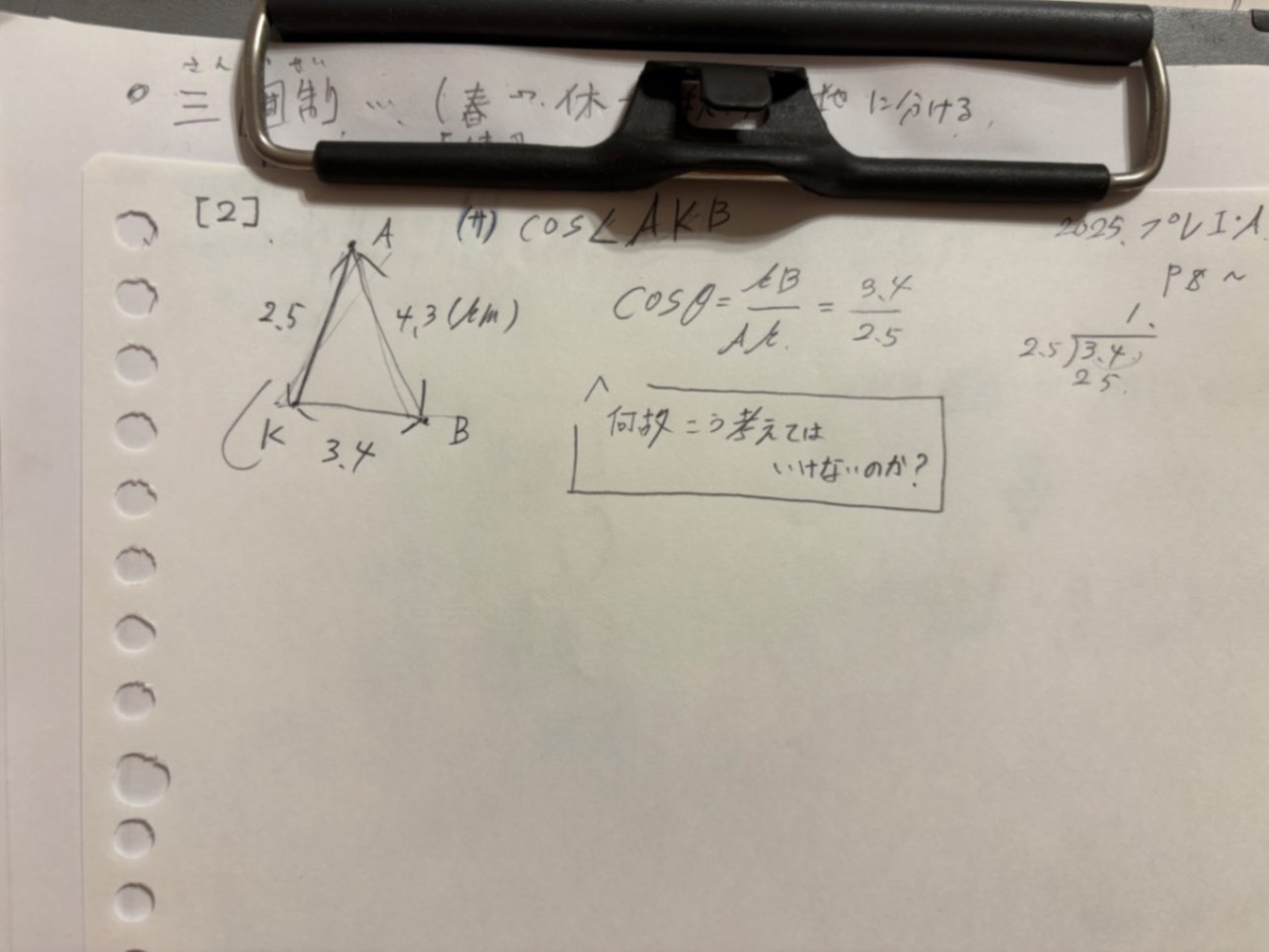
回答
ひなたさん、こんばんは。
三角比は直角三角形について、底辺、斜辺、高さの比です。
ですから、その図の辺の長さからはサインは無理です。
三角比は、角の大きさで決まってくる関数として考える時は直角三角形からはなれても決まります。あなたがどこまで学習しているのかが分からないので何とも言えませんが、鈍角の三角比が入ってくる時点からは座標平面の円で考えることになります。そのときは「辺の比」ではなくなります。
これでわかりますか?
解答ありがとうございます。 座標平面の円とは半径1の単位円の事で合ってますか? また、「辺の比」ではなくなる。という事がどういう事なのか上手く解釈出来なかったので、もう少し噛み砕いて下さると嬉しいです。 何卒お願い致します。
そうです、単位円です。単位円上の1点Pを定めると、∠xOP=θが定まり(θはx軸の正の方向から反時計回りにOPまで測ります。鈍角でもいいし、180°を超えていても良い)、Pの座標(x、y)も決まります。つまり、単位円上の点Pによりθ、x、yが定まります。このときθの三角比をcosθ=x、sinθ=y、tanθ=x/y と決めるのです。もうこの定義では直角三角形とは無縁の関数になります。θが鋭角の場合もこの定義に含まれています。 本によっては、単位円でなく、半径rの円で考えて、P(x、y)を用いてcosθ=x/r、sinθ=y/r、tanθ=y/xという説明も出てきます。 これだけでは分かりにくいと思います。教科書や参考書などお持ちなら、「三角比の拡張」「鈍角の三角比」あたりをよく読んでください。あるいは https://kou.benesse.co.jp/nigate/math/a13m0302.html など、「三角比の拡張」「鈍角の三角比」で検索すればいろいろ出てきますよ。
解説ありがとうございます。 三角比の単元や添付して下さったリンクを参照し、納得できたと思います。
それならよかったです。またどうぞ!