空間ベクトル　球

ありがとうございます！y座標、ｚ座標は変わらないと言えるのはなぜでしょうか？ 後半はなんとなくわかりました、、

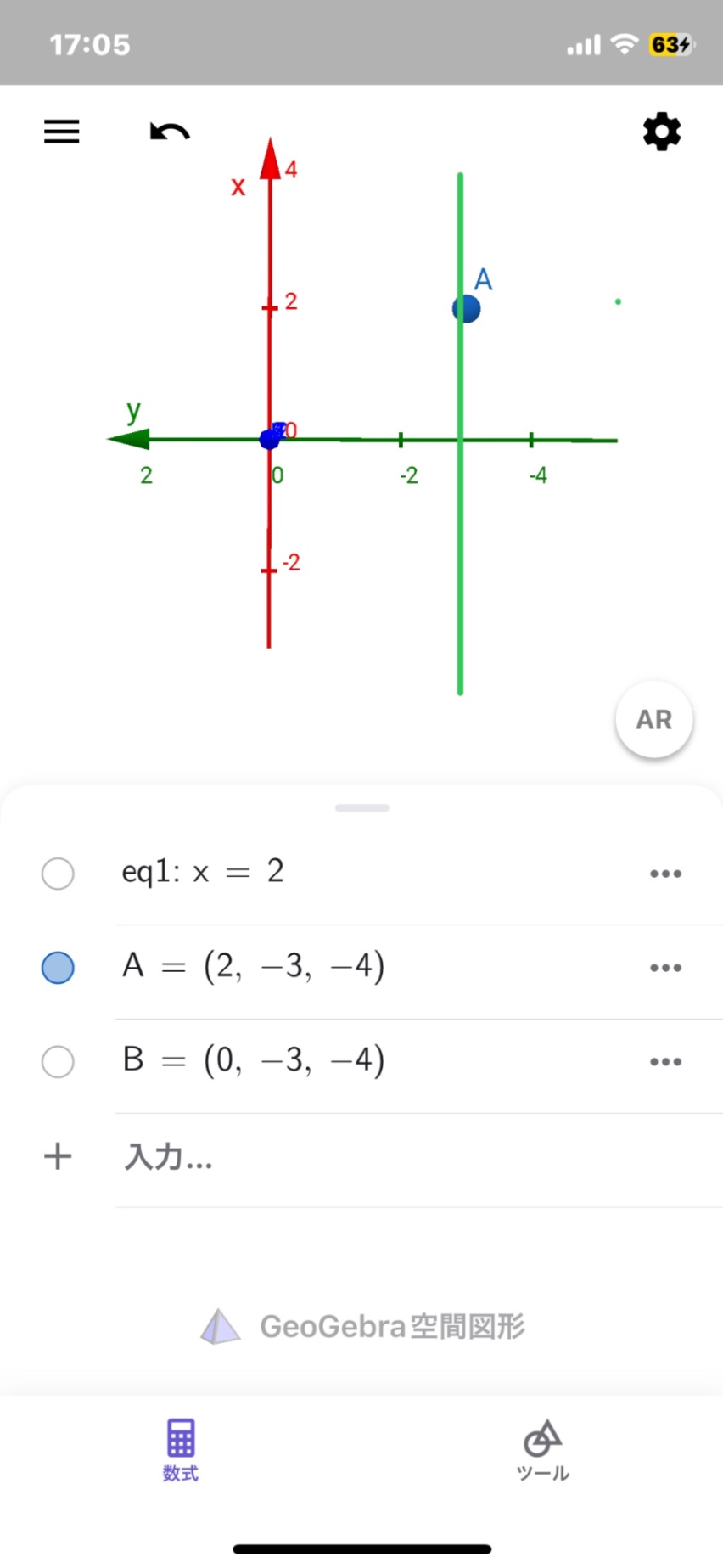
写真見ました。はい、ｘ＝０、ｙ＝－３、ｚ＝－４という点です。 簡単のために２次元のｘ、ｙ平面で考えると、点（ｐ、ｑ）からｘ軸に垂線を引いてその交点の座標はｙ座標が０になって（ｐ、０）になります。ｙ軸に垂線を引くと、ｘ座標が０となり（０、ｑ）になります。 空間内のある点からｙｚ平面に垂線を引きます。その垂線はｙ軸にもｚ軸にも垂直です。そのときはｘ座標が０になります。ｙ、ｚ座標はそのままです。これじゃ説明にならないか。点（２、－３、－４）を通りｙｚ平面に平行な平面αを考えます。ｘ軸とは２のところで交わっていますよ。点（２、－３、－４）から垂線を引くっていうことは、平面αをｘ軸に沿ってｙｘ平面に近づけていくっていうことです。すると点（２、－３、－４）のｘ座標だけがどんどん０に近づいて行き、ｙ、ｚ座標は変わらない……う～ん、言葉で説明するの、大変だぁ。自分の部屋で３つの面が交わるような隅っこで、ｘ、ｙ、ｚ軸が考えられるでしょ。指で点を作ってどれかの面に垂直に動かしてごらん！

ありがとうございます！ なんとなくわかりました！ ちなみに球の問題を解く時は図示して考えたらいいんですか？ 例えばこの問題を解答みたいに図示しないでやるならどうすればいいんですか？？

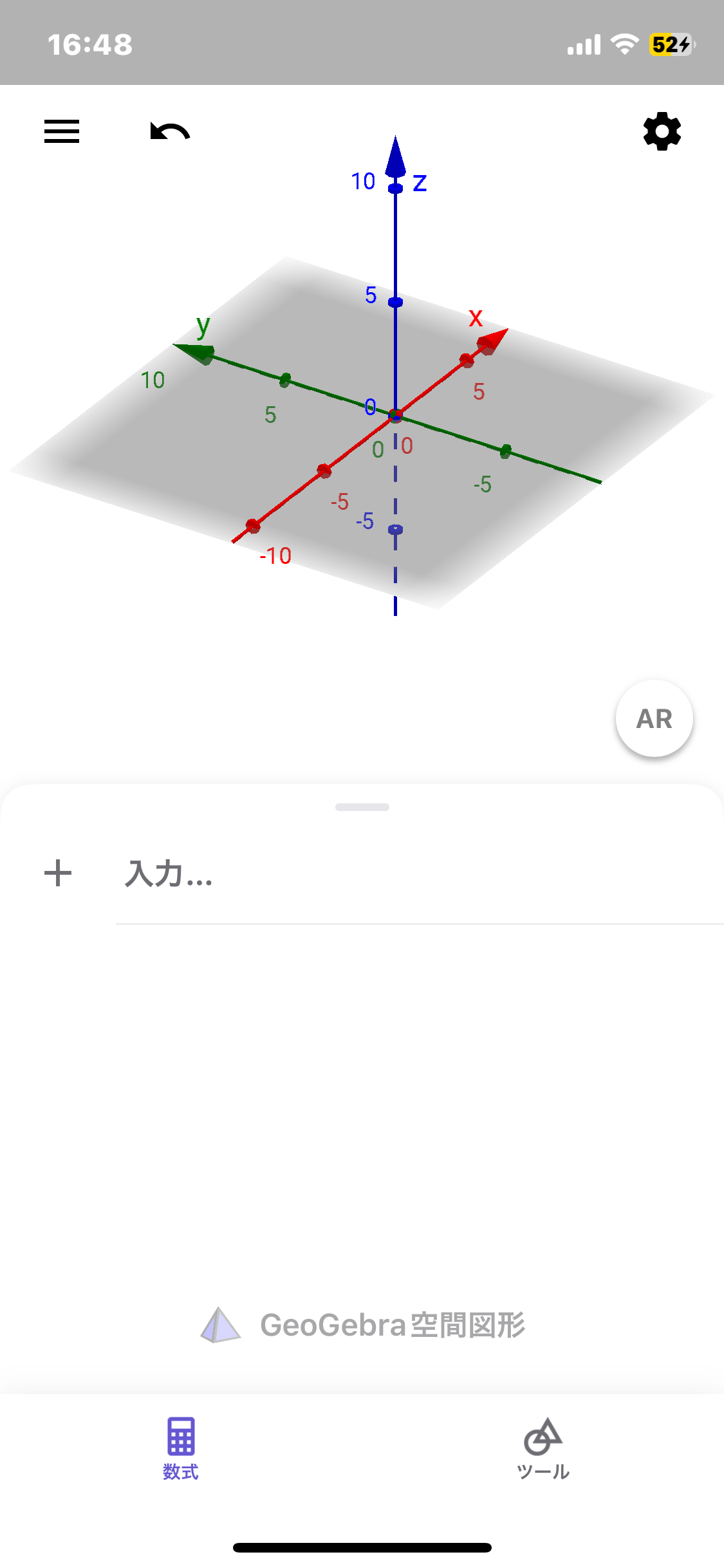
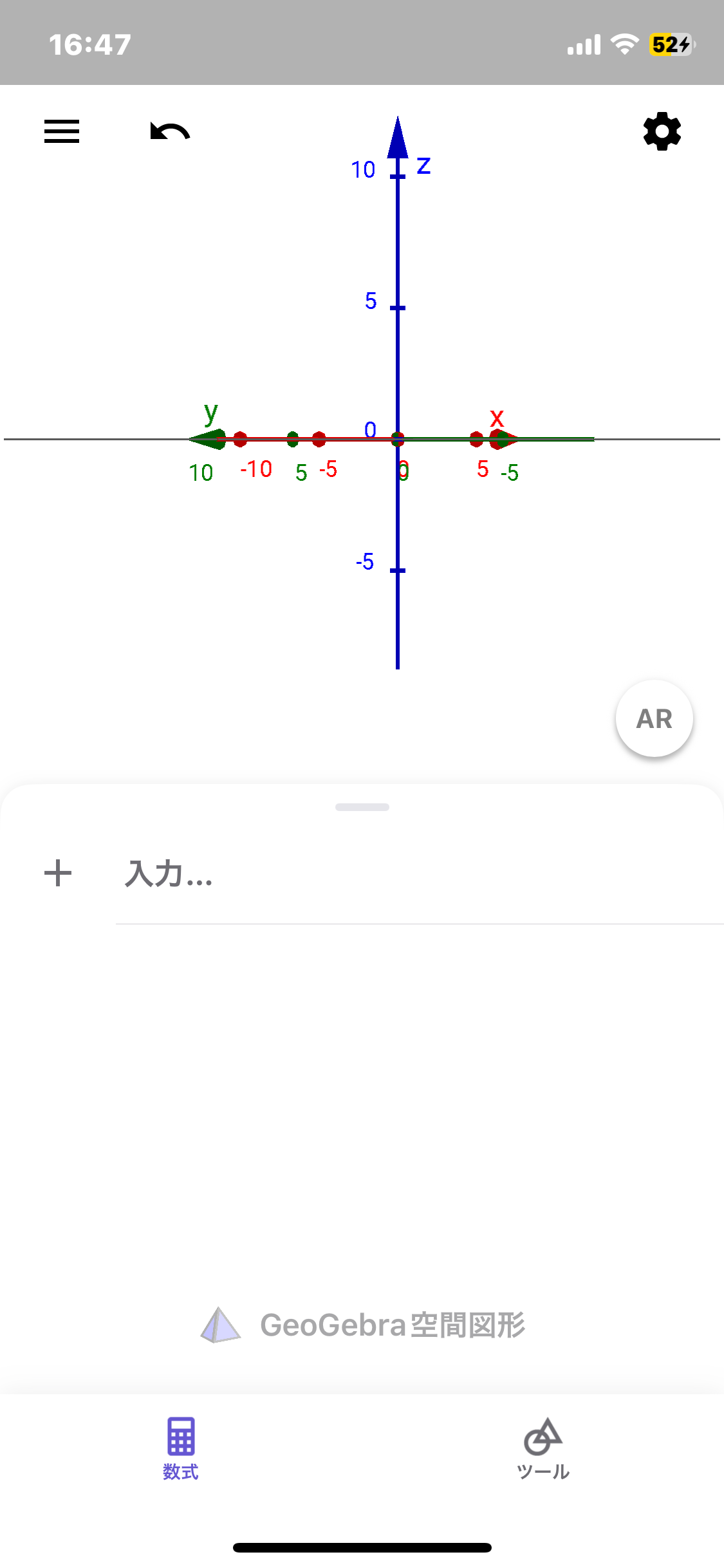
アプリで座標空間を動かしてみました。 なんとなくイメージがついた気がします。 一枚目のような座標空間を2枚目のように真横から見て考えているということですよね また緑の直線上にある点はすべてYZ座標が（−3,-4）ということですよね、、 考えてみると座標平面の時と同じ感じではあるような気がしてきました イメージするのが難しいですが、、

そんなことができるのですね！そごいです。スマホで動くの？