このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
空間ベクトル球2
途中でつまづいたので教えて欲しいです


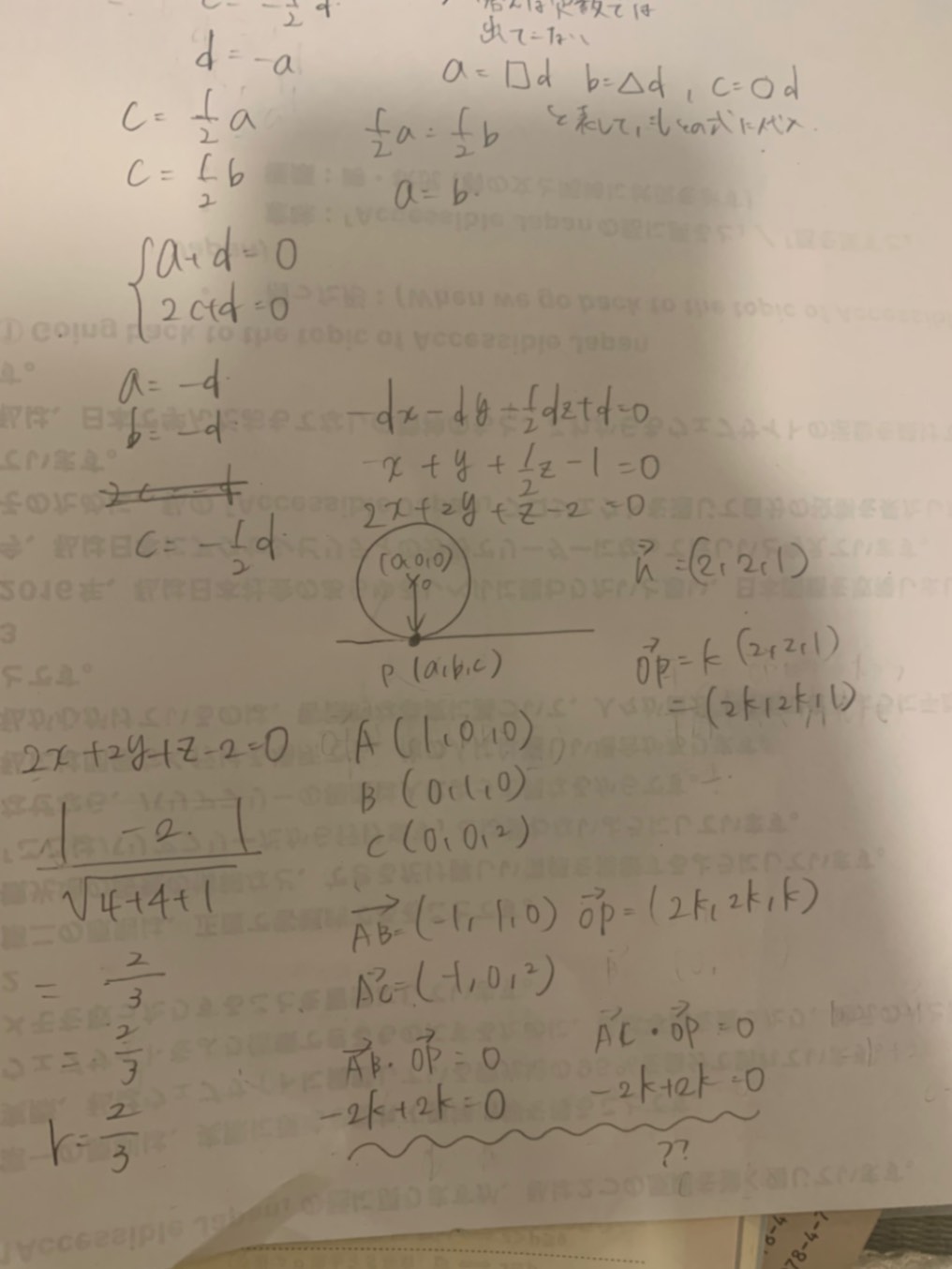
回答
百花さん、こんばんは。
空間図形で苦労しているようですね。空間を想像する力を養えるといいのですが、なかなか個人差があって、うまく想像できない人もたくさんいますが。
1枚目の写真の緑のところ:これはもう図を書くしかないです。3次元は書けないから、2つの球の中心を通る面で切った断面を想像してください。図を添付しました。断面では球はそれぞれ半径が√5と2√2の円になります。図のように中心をA,Bとし、交点をPとします。2つの球が交わってできる円はこの図では見えません。Pが直線ABを中心にぐるっと1回転してできる円になりますが、この方向からでは見えません。PからABに垂線を引いた足をHとすると、交わってできる円の半径がPHになるのは想像できますか?ここまでわかったら、この問題は平面図形の問題になります。△PABは3辺の長さが分かっています。このときPからABに引いた垂線の長さを求める問題になってしまいますよ!あとは3平方の定理でやります。やってみてください。もしやり方が分からなければ言ってください。ヒントを書きます。
2枚目の写真:rを求めよという問題でしょうか?平面と球が接している時、接点での球の半径はその平面に垂直になっているのはいいでしょうか?そうなると、けっきょく求めるものはその平面の原点からの距離(原点から平面に下した垂線の長さ)ということになるのわかりますか?この時点で、この問題は球とは無関係になり、平面と原点との距離を求める問題になります。まずは平面の方程式を求めますが、あなたのやり方で大丈夫です。方程式が3つで未知数が4つですから、どれかの文字(これだとd)を使って他の文字を表せば、最後にその文字で割ると方程式ができますよ。あとはベクトルを使うのが楽かなぁ。前の217番の問題みたい。あるいは、平面の方程式から法線ベクトルが分かるから、それを利用するとか。平面と点との距離の公式を知っているのなら、それで一発ですが。どれかでやってみてください。必要ならまた聞いてください。
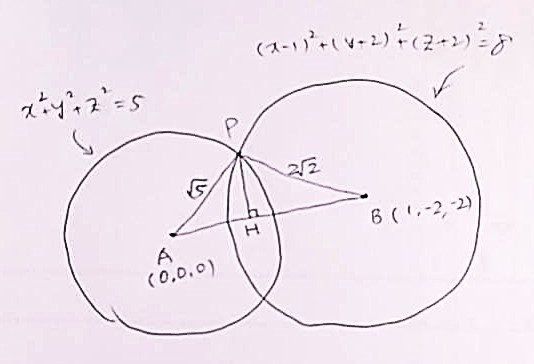
(2)がわかりませんでした、、 接点をPとしたら、OPベクトルも平面に垂直だから、 OPベクトルは法線ベクトルを使って表せると思いました また、OPベクトルは平面に垂直だから平面上の二つのベクトルと垂直で、内積がゼロになるというのを使うのかなと思いましたが、なんかわからなくなりました、、 理解力なくてすみません🙇♀️
公式を使って解くのはできました、、 でも今はベクトルを勉強中なのでできればベクトルを使って解く方法を教えていただきたいです😭
はい。ベクトルの→は省略しますよ。 平面の方程式から法線ベクトルが求まったので、ABやACとはすでに垂直になっていますから、それを使っても意味のない式になります! OPがまだわからないkを用いて表せたので、あとはPが平面ABC上にあるようなkを求めればいいです。平面ABC上にあるということは、OP=(1-s-t)OA+sOB+tOCであればいいので、二つの表現されたx,y,z座標が等しいという式をつくります。式が3つで未知数がk,s,tの3つだから解けますね。求まったkを使ってOPがえられ、その長さは計算できます。 これでどうでしょうか?
平面の方程式から法線ベクトルが求まったので、ABやACとはすでに垂直になっていますから、それを使っても意味のない式になります! →OPを法線ベクトルをk倍したものと考えているから平面と垂直なのは当たり前でそれを式にしても意味はないということですか??
球と平面が接する ↓ 法線ベクトルの端点が平面上にある ということでしょうか?