このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
円と放物線の接点



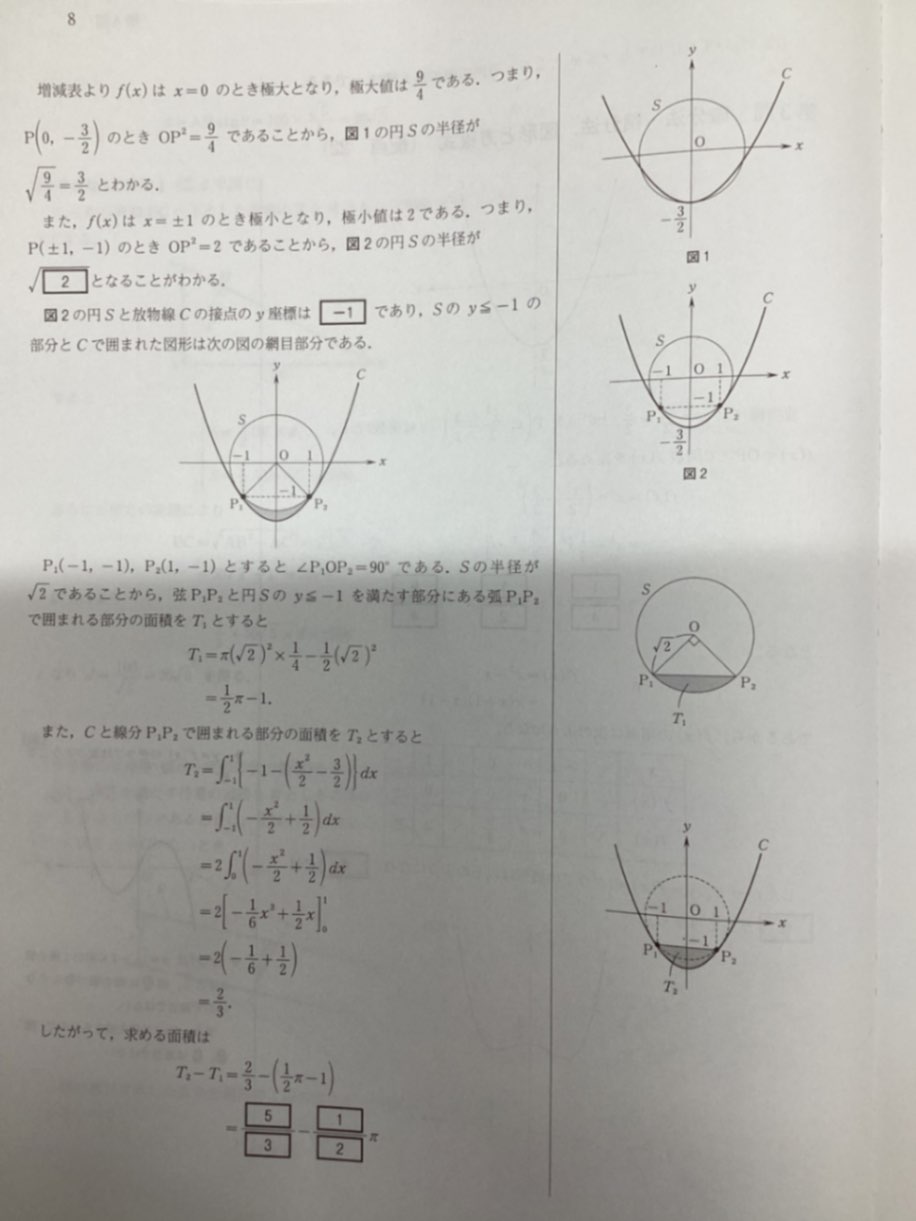
回答
くさぼうぼうさん ご回答ありがとうございます。いただいた説明で、解法の目的が理解できました! ただ、もう一つお聞きしたいことがあります。この解法は極値の1/2乗が円の半径になることの厳密な理由づけになっているのでしょうか。 問題では厳密な図があるため、接点の前後でOPの大きさが切り替わることに納得できますが、図を自分で描かなければいけない場合に、この図形的判断を根拠にするのは厳密でないように感じます。 この問題の場合、極値の場合のみ、必ず接していると判断できる根拠はあるのでしょうか。 教えていただけると嬉しいです。
なるべくていねいな図を書くことは大事です。図から得られることはたくさんありますからね。たぶんたいていの人は極値の1/2乗が半径だというとああそうか、となるところを、あなたはきちんと考えるかたで素晴らしいです。 2つの曲線が接している時は、それぞれの接線が一致しているのはいいですか?ですから法線も一致しています。円の法線は中心を通ります。よってf(x)=OP²が極値を取るところで法線は原点を通ります。だからOP²の極値は半径の2乗になっています。 これでどうでしょうか?
説明が不十分でした。追加しますね。 放物線上の点Pと原点との距離が極小となるような点が存在しました。その点と原点との距離を半径として、原点を中心とした円を描けば、その点以外では円の外になり、その点のみ1点が共有されています。つまり、そうやって描いた円と放物線は接しています。この後、上のコメントの後半がつながります。 変な書き方でスミマセン。
くさぼうぼうさん なるほど、その点で円と放物線の接線が一致している(両者が接する)ようなPについて、 ・OPは円の法線の一部であり ・円の法線が円の中心=原点を通る ことから、OPが円の半径になるのですね! 2つ目のコメントのご説明を ・放物線と円の、ある1点の共有点の左右で放物線と円の上下が入れ替わっていなければ、その共有点は接点だといえる ・f(x)が極値をとるPはこれを満たすので接点である …ということだと解釈し、納得できたのですが、この認識はあっているでしょうか。
グラフが滑らかな曲線であれば、それでいいです。ただし、一般的には必ずしも上下が入れ替わらないとはいえません。変曲点での接線は接点でグラフと接線の上下が入れ替わリます。
今回は円と放物線同士の関係で、変曲点が絡まないためこのように判断できるのですね。一般の場合の定義もきちんと把握するよう気をつけます。 何度も疑問に答えてくださり、ありがとうございました!おかげさまでとても理解を深めることができました。