このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
三角関数
写真の問題(2)についてです。
写真4枚目の解説に書き込んだ「?マーク」の部分がなぜその様に式変形しているのかが分かりません。
解説お願い致します。
【写真】
1枚目→問題
2枚目→問題
3枚目→解説
4枚目→解説
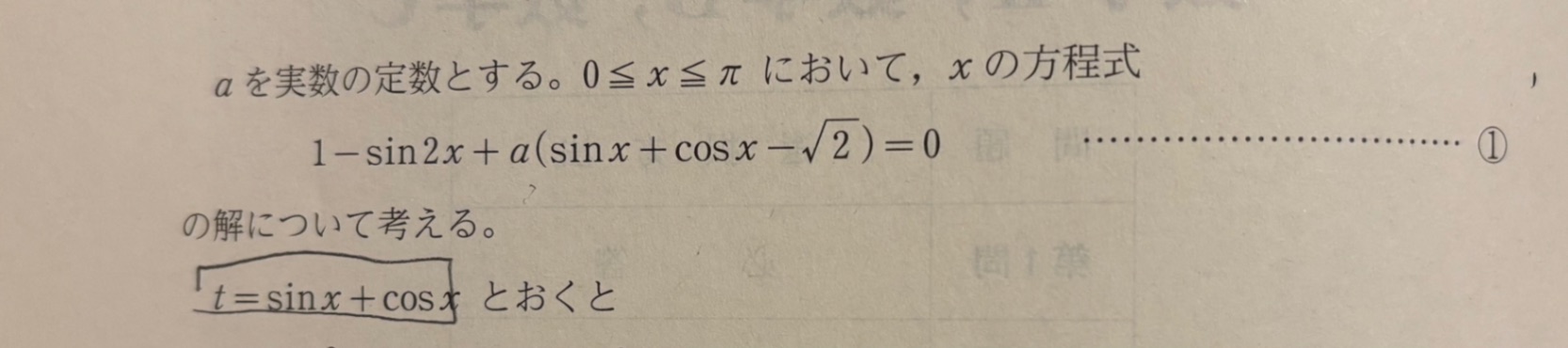

回答
ひなたさん、こんにちは。
④の式は見た目が悪いので、書き換えてみます。
$\theta=x+\dfrac{\pi}{4},t=\dfrac{a-\sqrt{2}}{\sqrt{2}}$ とすると
$\sin \theta =t$ …④という単純な式です。
変数θ(=$x+\dfrac{\pi}{4}$)の取りうる値の範囲を調べたのが、1番目の?の式です。
xの範囲の式にπ/4を足しました。
つまり $\dfrac{\pi}{4} \leqq \theta \leqq \dfrac{5}{4}\pi$ かつ $\theta \neq \dfrac{\pi}{2}$
ここはいいでしょうか?
次の?について。
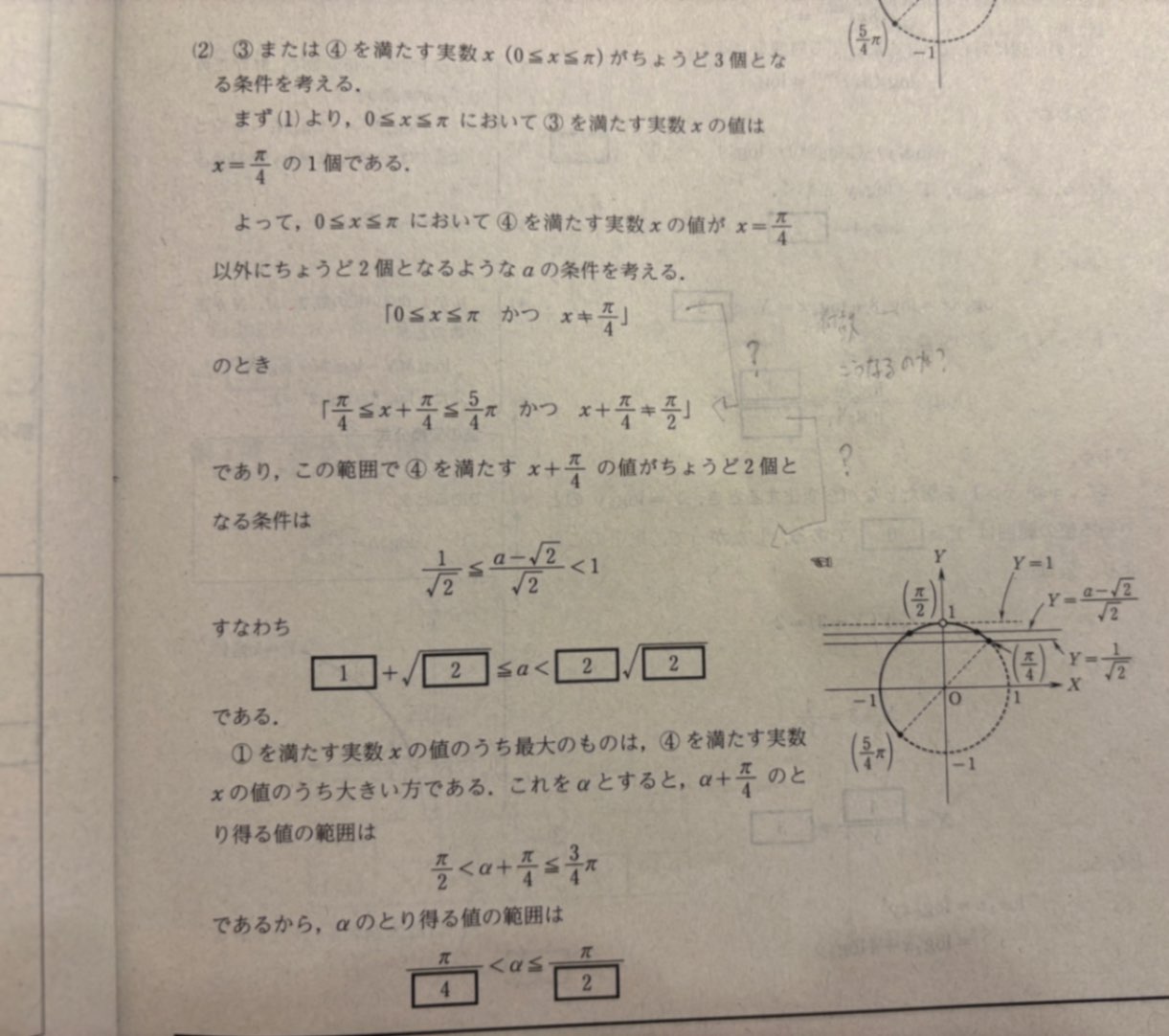
方程式 $\sin \theta =t$ …④が範囲 $\dfrac{\pi}{4} \leqq \theta \leqq \dfrac{5}{4}\pi$ かつ $\theta \neq \dfrac{\pi}{2}$ で、2つの解を持つようなtの範囲を調べますよ。
すると、そこに書いてある図のように(図のYはここではtになってます)、動径の動ける範囲は太線のようになり、その範囲でY軸上に現れるサインの値tにたいしてθが2個得られるのは、tが $\dfrac{1}{\sqrt{2}}$ 以上で1より小さいとき時だと分かります。って、分かりますか?tが1/√2以上で1より小さい値だとそれを満たすθが範囲内に2つありますね。
よってtすなわち$\dfrac{a-\sqrt{2}}{\sqrt{2}}$ が$\dfrac{1}{\sqrt{2}}$ 以上で1より小さいとき、θすなわち$x+\dfrac{\pi}{4}$が2個得られるのです。すなわち解xが2個得られるわけです。
その図はもう少し上の方に書いてほしいですね。その図がもろもろの根拠になっています。
これで大丈夫ですか?あなたが引っかかっている状態がはっきりわからないので余計な説明やら説明不足やらがあるかもしれません。コメント欄になにか返事を書いてください。
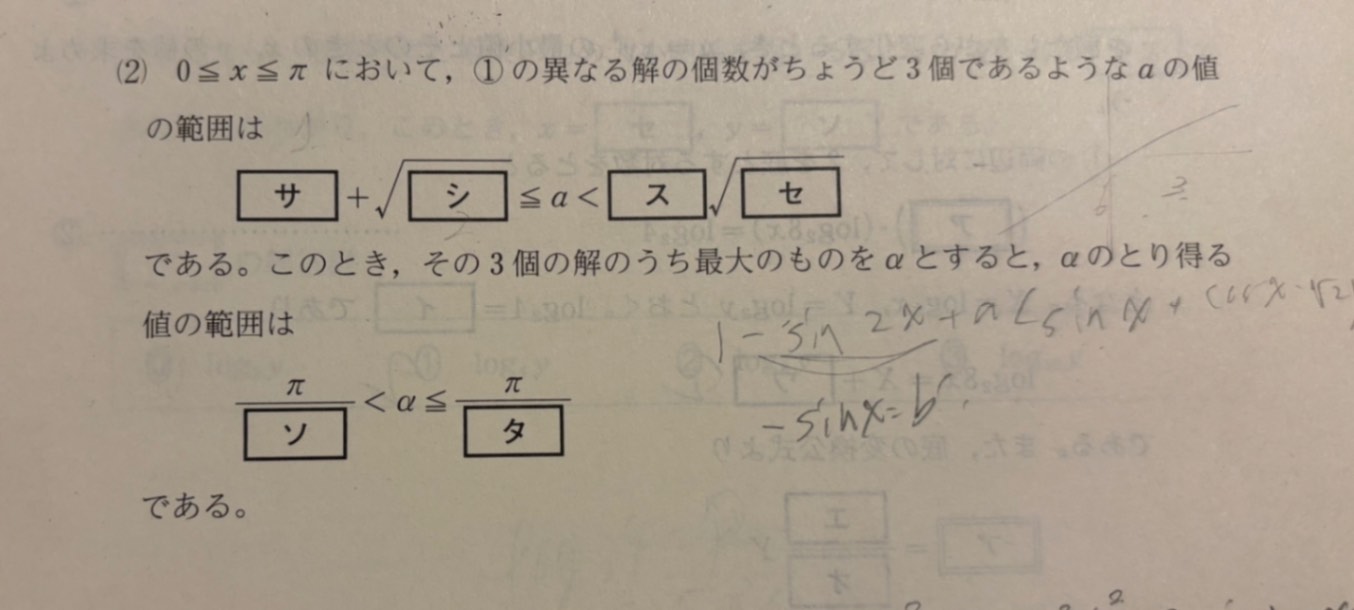
回答ありがとうございます。 この単元の基本問題を解き直したりしながらぼうぼうさんの解説と問題の解説を何度も読み直して、ご解説頂いた部分は理解出来たと思います。 ありがとうございます。 追加の質問になってしまうのですが、 その後の問題の「αが最大となる範囲」について解説では「xの値が大きくなる方」と書かれていますが、 「π/2〜3/4π」ではxの値がマイナスになりますよね。 でもそれは➀の式より定められた範囲「α+π/4」に則って表記しているので、それを元の範囲「0≦x≦π」で考えた時、動径の有効範囲内でxの値がプラスになるのは 「π/4〜π/2」である、という解釈で大丈夫でしょうか?
いや、大失敗しました!ゴメンナサイ、文字tははじめに使っていたんですね。私が書いたtはbとか、他の文字にしてください。わかりにくく書いてしまいました。問題文のtと私が書いたtは全く関係ない別物です。質問された個所しか見ないで回答してゴメンナサイ! 次の質問の答はちょっと待ってください。
追加の質問: ・αはxの解の内の大きいほうです。ですからxと思っても差し支えないです。 ・「π/2〜3/4π」はα+π/4すなわちx+π/4の範囲ですので、xは負にはなりませんよ。 ・x+π/4の範囲あるいは同じことですがα+π/4の範囲がπ/2〜3/4πなので、xあるいはαの範囲がπ/4〜π/2ということです。その解釈でいいのだと思います。
返信遅くなり申し訳ありません🙇 追加の質問にも丁寧にご対応下さりありがとうございます! お陰様で理解出来ました。
それならよかったです。