確率の対称性

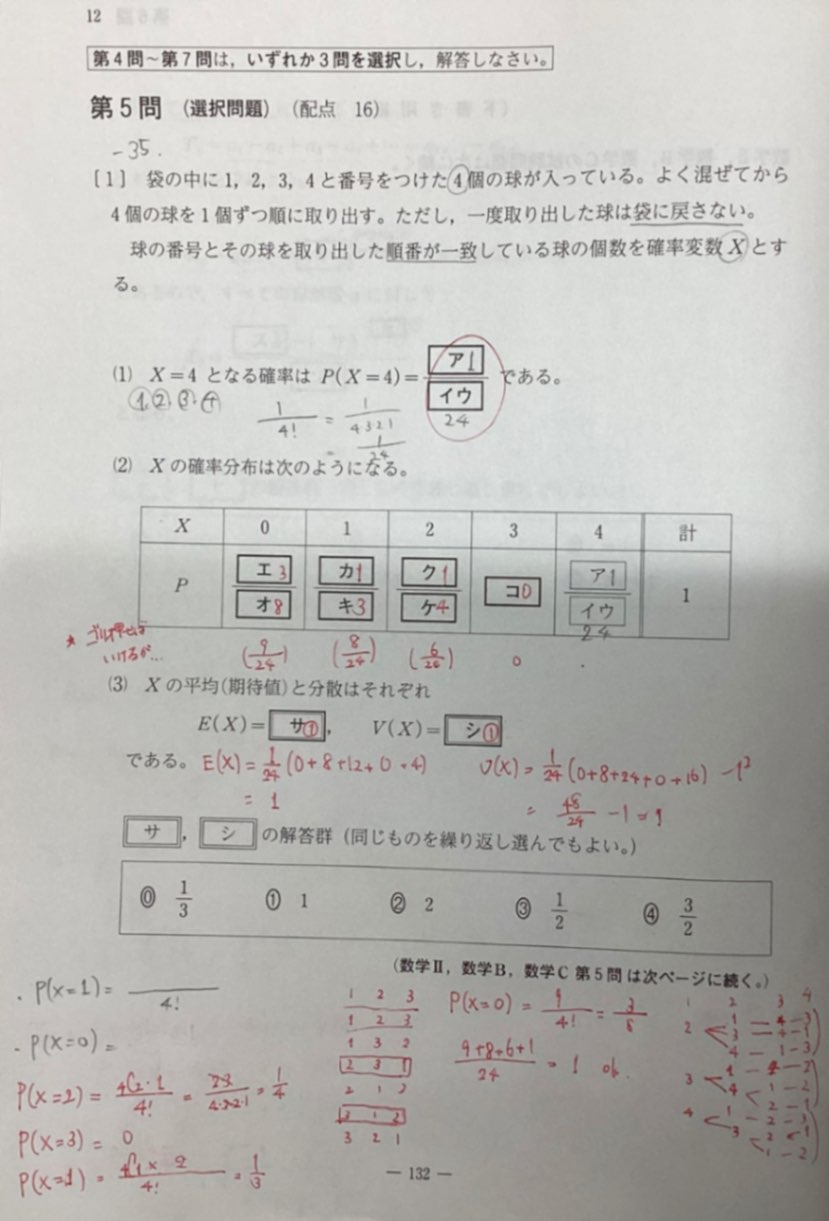
こんばんは！質問失礼します。 ・1、2、3、4と番号をつけた4つの球が入っている袋から1つずつ球を取り出すとき ・球の番号と取り出した順番が一致している球の個数を確率変数Xとする という条件でXの確率分布を求める問題です。 球の番号と取り出す順番が一致するパターンの数がどの番号でも対称性をもつ理由が分かりません。 (解答では、例えばX=1のとき、「1番目に番号1の球をとって、ほかは一致しないパターン」のみを調べ、これを番号2、3、4の球が一致するときにも当てはめていると思います) どうすればこういった確率の対称性に気がつけるのでしょうか？ 教えていただけると嬉しいです。よろしくお願いします🙇

Maru Masa さん、こんばんは。 質問は失礼なことではありませんっ！ 遠慮なく質問してくださいね。 対称性っていうのとはちょっと違うかとは思いますが、数字の１，２，３，４や１回２回３回４回には特に区別も優劣も軽重もなく、まったく対等だからとしか言いようがありません。順番なんてかんがえなくても、取り出す取り出し方は単に順列でしかないです。「１から４までの数が書かれた４枚のカードを裏返して１列に並べ、開けてみたら数字と位置の番号が一致していた枚数をXとする」と同じです。 というか、解答でも「他の数でも同じだから」とは書いてなく、まず「１回目に１が出てX=1となるのは…」を考えた後「２回目に２が出てX=1となるのは…」「３回目に３が出てX=1となるのは…」とか考えて調べていくと「ありゃ、同じだぁ！」と気が付く程度のものです。たぶん「２回目に２が出てX=1となるのは…」を調べる時に気が付けばラッキーというぐらいです。 ごめんなさい、こんな回答しか思いつかず、納得していただけるか心配です。必要ならもっと突っ込んできいてください。コメント欄になにか返事を書いてください。