x=f(y)の形の積分

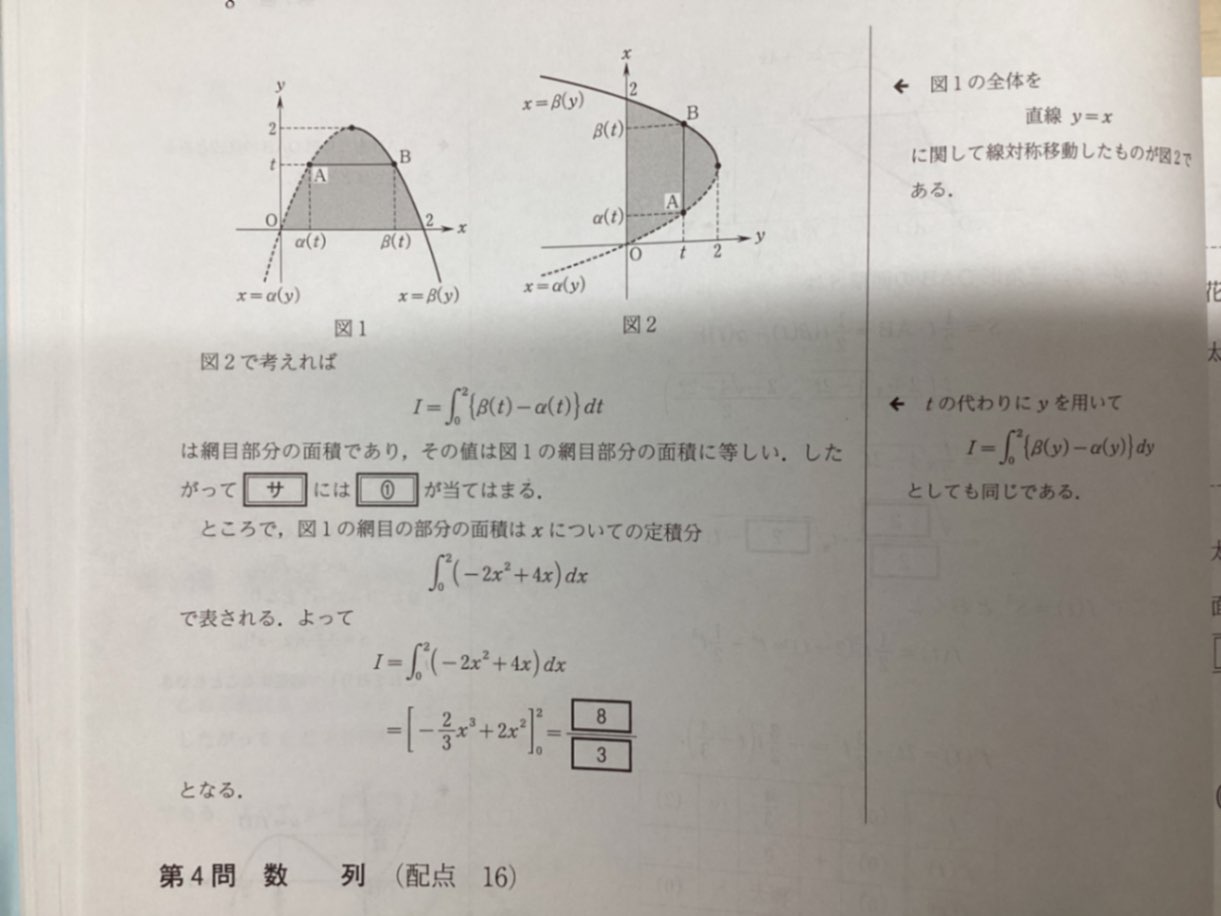
こんばんは！ 微積分の問題中の誘導および解答が意味しているところを教えていただきたいです🙇 ⚫︎分からないところ ・添付画像2枚目(問題(2))右ページの太郎の発言を図に表した場合、同ページ下の図①になるということだと思ったのですが、解答を読むと、図①のx軸とy軸を入れ替えた図2が提示されていて、この網目部分が$\int_{0}^{2} ({β(t)-α(t)}) dt$を表すと書かれています。なぜx軸とy軸を入れ替えて考えているのでしょうか。 ・また、この積分$\int_{0}^{2} ({β(t)-α(t)}) dt$はy=0からy=2まで、放物線Cをy軸方向に積分しているということですか？ 教えていただけると嬉しいです。よろしくお願いします！

Maru Masa さん、こんばんは。 初めの質問の回答： あなたが言うとおり、①のずでいいのです。その図でｙ方向（ｔ方向）の積分が理解できて、斜線部の面積になることが分かる人には図２は不要ですよ。ただ、横軸方向の積分の方が一般的なので、たぶんその図を書いて、β(t)－α(t)をｙ軸（t軸）方向に積分する方がわかりやすいし、2枚目の写真の左ページにある「定理」と同じ形にしたかっただけかと思います。分かる人には不要です。 2番目の質問の回答: そのとおりです。ｔというのは「ｙの値がｔ」という意味合いなのでｔで積分していますが、ｙで積分しているのと同じです。 これで大丈夫ですか？