統計的な推測

δ/√nは標本標準偏差を表すので、標本標準偏差5を用いてそのまま計算してみたのですが違いました。初めの写真の問題と次の問題の違いは何でしょうか。

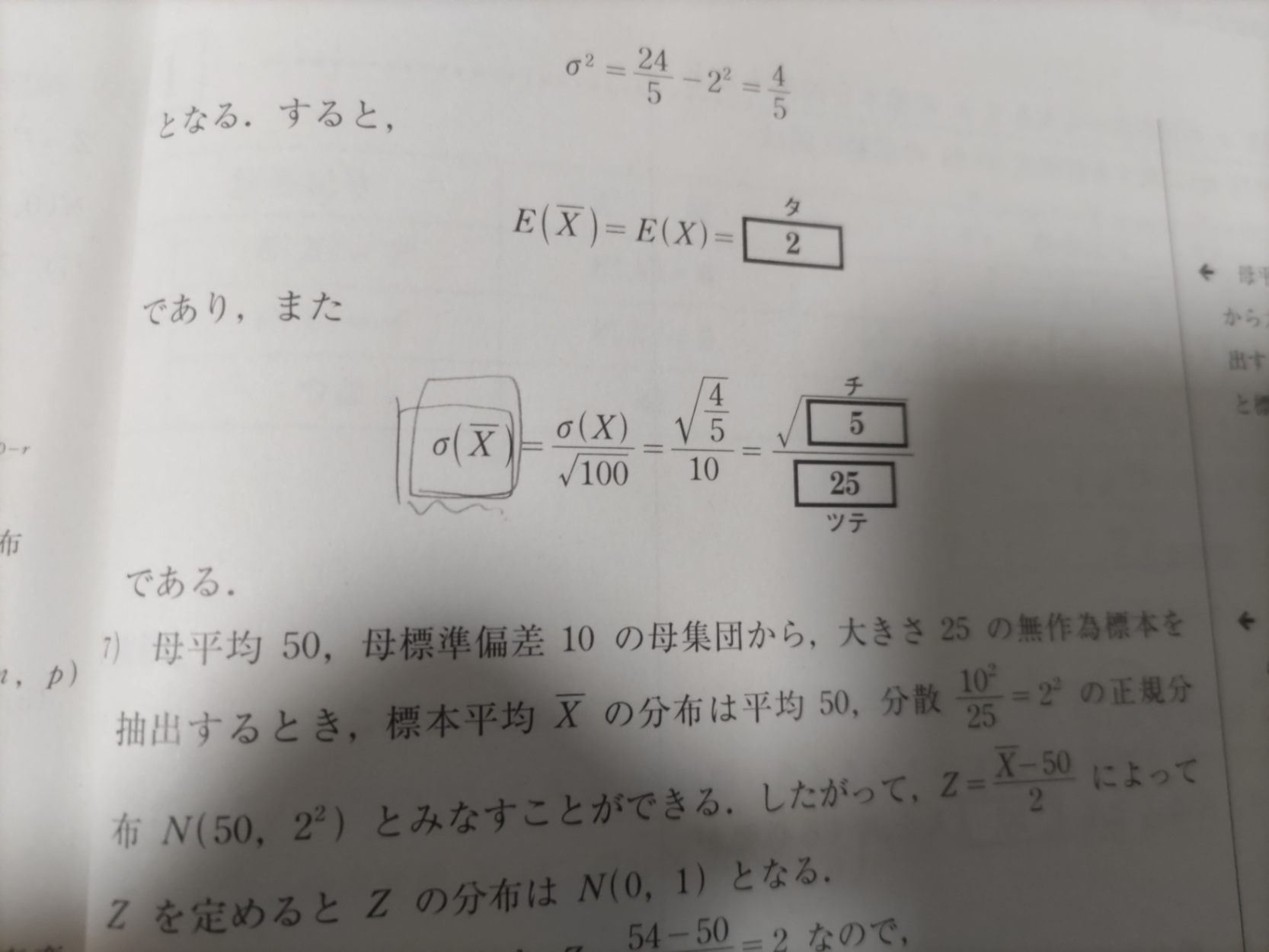
か い さん、こんばんは。 そのあたりの質問は多いです。 あなたの質問個所がつかめないのですが、初めの方の問題のどれですか？タチツテのどれ？ 「δ/√nは標本標準偏差を表す」のではなく「δ/√nは標本平均の標準偏差を表す」だと思います。 しっかり把握しなくてはいけないのは、標本平均の平均、標本平均の標準偏差と、ある標本の平均、その標本内での標準偏差の区別です。 標本調査をするとｎ個のデータ $t_1,t_2,t_3,\cdots t_n$ が得られます。 この標本のｎ個の値の平均が X です。このｎ個のデータの標準偏差を$\sigma '$ としておきますよ。 何回も標本調査をすると、各標本ごとに平均Xは変わります。標本調査をｍ回やったとして、それぞれのXの平均が $E(\overline{X})$ です。これは母平均に等しくなります。ｍ個の $\overline{X}$ の標準偏差は $\dfrac{\sigma}{\sqrt{n}}$ ですが、それと$\sigma '$ は別物です。 ｎが大きいときは標本は母集団に近くなりますね。ですから標本の標準偏差は母集団の標準偏差に等しいと見て差し支えないですね。 これでどうでしょうか？ 大事なのは、「標本の中の平均、標準偏差」と「標本平均の平均と標本平均の標準偏差」をしっかり区別できることです。 これでどうでしょうか？コメント欄になにか返事を書いてください。