このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
2次関数 aの範囲


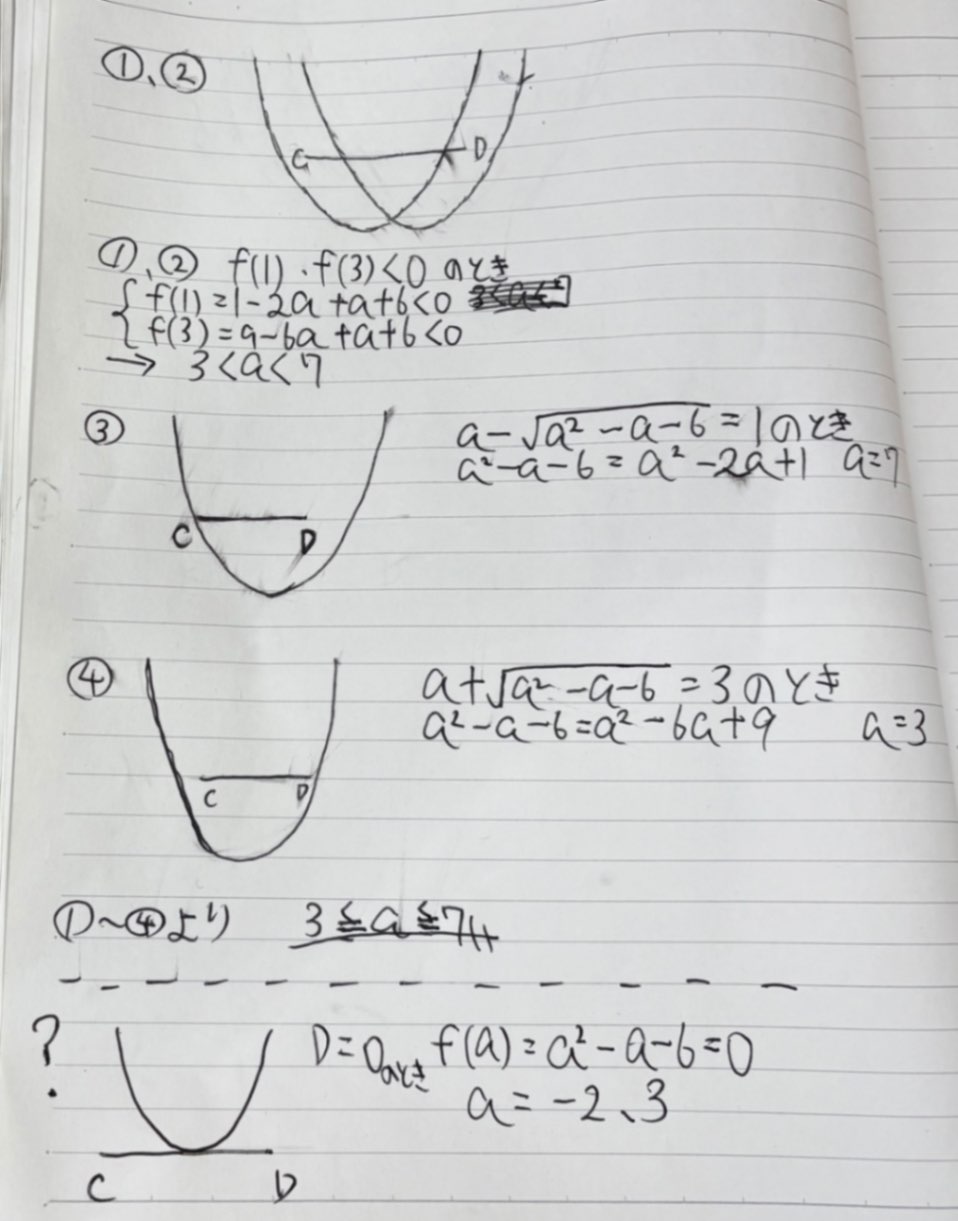
回答
くさぼうぼう様、回答ありがとうございます。 「三角比の問題(1)再質問 2025年12月12日15:12にコメントしたもの」とは 三角比の問題(1)再質問 2025年12月12日15:12 に投稿したやり取りの中で、草ぼうぼう様の2025年12月13日17:55時点でのコメントに対し2025年12月14日1:15に返答したものです。 ①、②における、積の2次不等式は見当たらないとありますが、なぜ、f(1)=0×f(3)にしなければならないのでしょうか?特に「あくまでも異符号であること、すなわち積が負ということ」が理解できません。 ③、④はそれぞれ、③放物線がCを通り、Dを通らない場合、④放物線がCを通らず、Dを通る場合です。 xは解の公式で求めましたが確かにそのやり方が楽ですね。 またD=0かつその重解が1と3の間の場合で求めたa=−2は考慮しなくてよかったのでしょうか? なお場合分けは全部で5回行うということでしょうか?
「2025年12月12日15:12にコメントしたもの」ではなく、「2025年12月14日1:15」ですね。それは拝読しましたが、あなたが自分で確認したことが書いてあって、特に質問なのではないと思いまして回答していません。失礼しました。そのコメントについては「2つのt」ってわからないです。tはあくまでも1つですよ。 次。CDの中間で放物線が線分を横切る状態をまず考えていますよ。この時はただ1つの共有点を持つことは分かりますか?そのように横切るときの特徴はX=1とX=3のときに放物線が線分(x軸の一部)の上と下にあるときです(どちらが上、どちらが下でも可)。放物線がⅹ軸より上にあるときは関数値が正、下にあるときは関数値が負ですよ。つまりf(1)の値とf(3)の値が異符号の時だと分かります。よって①②を一緒にした条件式はf(1)f(3)<0つまり、(7-a)(15-5a)<0、簡単にして(a-7)(a-3)<0という2次不等式を解くことで3<a<7が得られるのです。あなたの2つの式からはa>7とa>3が得られるだけで範囲は求まらないですよ。 a=-2のとき、実際にやってみて、それが適するかどうか確かめましたか?a=-2のときの重解はx=-1なので、線分CDとは共有点になりません。 場合分けの個数は、答案の書き方、まとめかたで異なります。①②をいっちょにした場合は4つでいいかな? これで大丈夫ですか?
コメントありがとうございます。 f(1)×f(3) <0の仕組みは、なんとなくわかったような状態です。 確認なのですが、f(1)=0,f(3)=0の式はC(1、0)・D(3、0)を代入した上で式が成り立っているのですよね? コメントお待ちしております。
それは点C,Dを通るときの話ですね。その考えでいいです。