このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。

積分　面積の対称性

    Maru Masa (id: 4390) （2025年12月17日21:24）
    0 0
    こんばんは！ 積分した面積の対称性について言及している模範解答について、解説をお願いします。 添付画像の問題(2)の(ii)［ヌネノハ］を解いています。S_1=S_2となることを示したいのですが、模範解答の黄色くマークした部分の説明が分かりません。 S_1、mの傾きがt=1について対称であることは理解できたのですが、そのことがなぜS_1=S_2に繋がるのでしょうか…？ ご回答いただけると嬉しいです。

    IMG_0713.jpeg

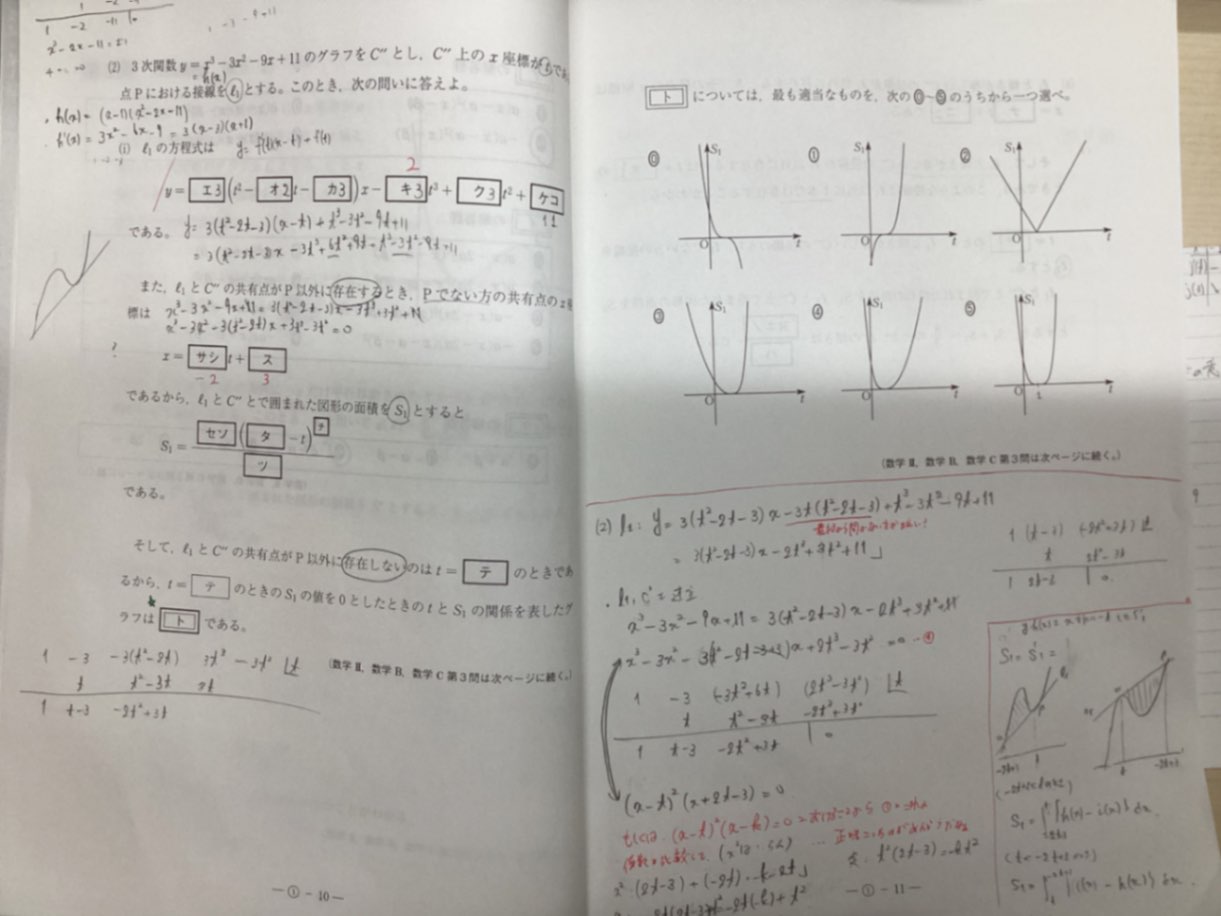
    IMG_0714.jpeg

    IMG_0715.jpeg

    IMG_0716.jpeg

    回答

    くさぼうぼう : (id: 1236) （2025年12月18日10:56）
    0 0
    Maru Masa さん、こんにちは。 ま、ｔ＝１に関して対称だということを使わなくても、地道にやれば出ますがね。 積分で求める両端の部分と、中央部の平行四辺形の面積を足したら8/3だという式で求まります。 でもその前でせっかく12分の1公式を作ったのだから…ということなら、S₁、S₂のそれぞれに1/12公式を適用するのでもよさそうです。 解答を書いた人は対称性を使ってもっとスマートにやろうとしたのでしょうね。 直線はそのどの点に対しても対称。面積も（１－ｔ)⁴で決まるのでｔ＝１について対称。これが分かると、たとえばS₁、S₂をy軸に平行に超細かく等間隔で細切れにしたとき、ｔ＝１にたいして対称な長方形の面積はそれぞれ等しいはずです。だって直線のｙ座標も3次曲線のｙ座標も多少なので、長方形の縦の長さ（ｙ座標の差）も同じだから。よってそれらをすべて足し合わせたものは等しい（積分の原理から）です。 と、あれこれ書きましたが、あなたが知っておいて一番得なことは「3次曲線のグラフは変曲点に対して点対称な図形である」ということと、「変曲点における接線はグラフをまたぎ、それと同じ傾きの接線はほかには存在しない」「傾きが等しい接線は変曲点に対して対称」ということです。すでに知っておられたらごめんなさい。これらのことは計算するだけで証明できますので、まだやっていなければやってみて納得した方が便利ですよ。これらのことは入試で使っても大丈夫なことがらです。 このことを使えば、ｔ＝１のところは変曲点ですから3次曲線自体がｔ＝１に関して点対称です。接点ではない交点も対称な位置にあり、これでS₁、S₂を表す図形そのものが対称であることが分かり、だからS₁とS₂は等しいことは計算をするまでもなくわかります。 これで大丈夫ですか？
    Maru Masa (id: 4390) （2025年12月18日14:01）
    0 0

    くさぼうぼうさん なるほど、t=1について3次曲線も接線も対称であれば、S1とS2それぞれに、t=1について対称な高さの長方形ができて同じ面積だとわかるのですね。 ▶︎直線はそのどの点に対しても対称。面積も（１－ｔ)⁴で決まるのでｔ＝１について対称。これが分かると、たとえばS₁、S₂をy軸に平行に超細かく等間隔で細切れにしたとき、ｔ＝１にたいして対称な長方形の面積はそれぞれ等しいはずです。だって直線のｙ座標も3次曲線のｙ座標も多少なので、長方形の縦の長さ（ｙ座標の差）も同じだから。よってそれらをすべて足し合わせたものは等しい（積分の原理から）です。 この部分で質問させていただきたいのですが 「面積がt=1について対称である」⇒「3次曲線はt=1について対称である」ということで「その後に3次曲線のｙ座標も対称」と書かれているのでしょうか？

    くさぼうぼう : (id: 1236) （2025年12月18日17:48）
    0 0

    「「面積がt=1について対称である」⇒「3次曲線はt=1について対称である」ということで「その後に3次曲線のｙ座標も対称」と書かれているのでしょうか？」すみません、質問の焦点がよく分からないのですが。私の言葉足らずだったようですね。 3次曲線が変曲点に関して対称であることを知っているかどうかで、考え方の進み方が違うようですね。すみません。 もう一度ご質問を整理して書いていただけませんか？

    Maru Masa (id: 4390) （2025年12月18日18:27）
    0 0

    分かりづらい質問をしてしまいすみません！ 3次曲線が変曲点について対称であるという知識は持っていて、点対称になるから面積が同じということは納得できています。 知りたかったのは、模範解答では変曲点について対称という知識を使わず、面積のグラフの対称性からS1=S2を導いているように見え、その場合どう考えたらよいかということです。

    くさぼうぼう : (id: 1236) （2025年12月20日20:49）
    0 0

    たしかに。ちょっと乱暴な推論ですね。ま、解答を書いた人は変曲点について対称ということが頭にはあって、でもそれをまず示すのは面倒なので書かずに済ませようとしたのかも。ゴメンナサイ、その解答の解説がうまくできません。

    Maru Masa (id: 4390) （2025年12月22日22:26）
    0 0

    返信が遅くなりました。すみません！ まずは変曲点について対称であることをきちんと押さえることが大切なのですね。教えてくださりありがとうございます！

    回答する