このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
2次関数(3) 異なる二つの共有点
(3)
①の左辺をf(x)としたとき、y=f(x)のグラフを考えて、1≦x≦3の範囲に2つの異なる実数解をもつ、
つまり満たすべきaの条件式は、
① の判別式D>0
② 1<y=f(x)の軸<3
③ f(1)≧0 かつ f(3)≧0
の3つなので、①~③から得られるaの共通部分が解になる形で大丈夫でしょうか?
ちなみに答えはエになりました。



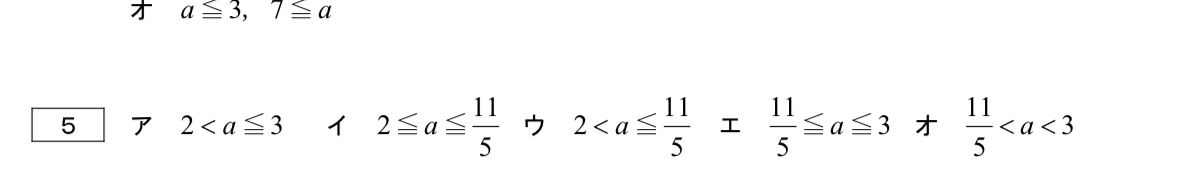
回答
こんにちは。
あなたのやり方で11/5が出ますか?ちゃんと問題を読んでますか?
あなたの解き方は、x軸の1から3の間で共有点が2個あるという問題の解き方です。でも、いまは、線分EFとの共有点ですから、それではだめですね。略図を書いて、必要な条件を探してください。
うまく見つからないようなら、またコメント欄に書いてください。