図形

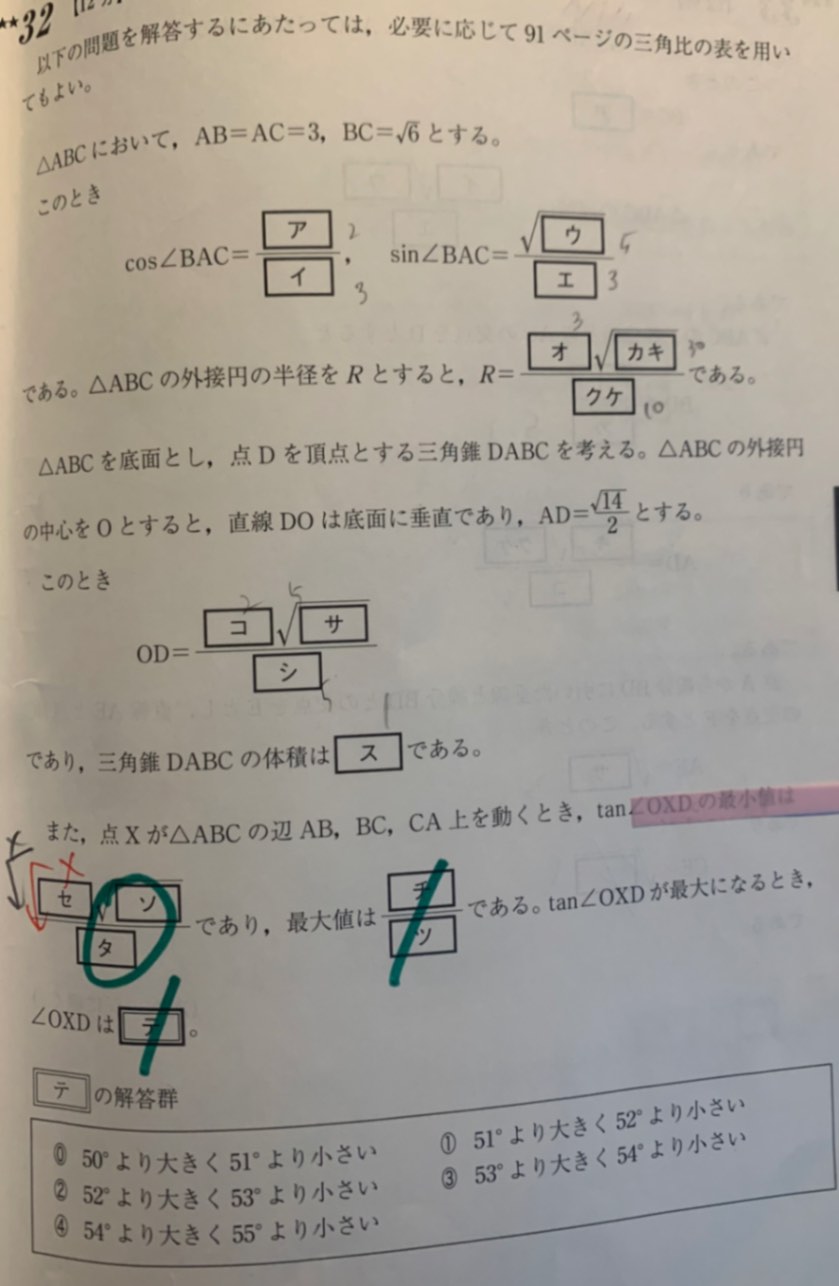
こんにちは。質問よろしくお願いします！ チ・ツについて、なぜoxが最小になるときXがabの中点またはacの中点にあるのか(bcとかではない理由)説明できません。想像すればなんとなくそうなんだろうなとはわかるのですが説明が....

$\tan \angle OXD = \frac{2}{\sqrt{5} OX}$ですね。 これが最大になるためには、分母が最小である必要があります。 分母が最小になる、$点O$から各辺に向かって一番近くなる点はどこだ？となります。 で、その点（$点O$から一番近くなる点）が今回は$辺AB,AC$の中点だったわけですが、なぜ中点になるのか。 $点O$がどういう点なのかを理解していれば、わかります。 さて、$点O$はどういう点でしょうか？ チクタク🕕️ チクタク🕐️ はい、$△ABC$の外心です。 三角形の外心の作図の仕方は覚えていますか？覚えてなかったら、調べてみてください。そしたら分かるはずです。 疑問点があれば、質問してくださいʘ⁠‿⁠ʘ 元旦からお疲れ様です👍️

まかろん さん、こんにちは。 $\tan \angle OXD=\dfrac{OD}{OX}$ で、ODは一定ですから、OXすなわちOから辺上の点までの距離が最短であればタンジェントは最大になりますね。 直線外の点と直線上の点との距離の最小値は垂線の長さになるのは大丈夫ですか？ あとはKeitaさんがお書きになっているようにOは外心だということから、あるいは△ABOはAO=BOの2等辺三角形ABOであるからOから引いた垂線と中線は一致し、辺の中点までの距離が最小と分かります。さらにABの中点、BCの中点、ACの中点のどれが最も短いかを調べればいいですね。 「(bcとかではない理由)」について。ABの中点とACの中点に関しては対称性から同じ長さであることは分かります。じゃ、OからABの中点までの距離とOからBCの中点までの距離はどちらが小さいのかを決めればいいです。 たぶん、この問題は穴埋め形式なので、そのへんはあれこれ図を書いたりして見当をつけるだけでいいのでしょうが、記述式で、あるいはあなたが納得するように書くには、「BCを外接円Oの弦と見る時、BCは△ABCの最小辺だから、弦ABや弦ACに比べてOからは最も遠い」ということです。これでも納得できないようなら、「BCの中点をNとする。△MBOと△NBOを比較して、MB＞NBですから、三平方の定理に当てはめれば OM²＝OB²－MB²＜OB²－NB²＝ON²よりOM＜ONである」という根拠ならどうでしょうか？ たぶんこのような考察は不要なのでしょうが、あなたがそこに引っかかっているかもしれないと思い書きました。 これで大丈夫ですか？下のコメント欄になにか返事を書いてください。