このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
グラフ
最後の問題についてです。
一応全部解いてみたんですけど、式が違うのか答えを一致しません。
解説お願いします🙏🙏

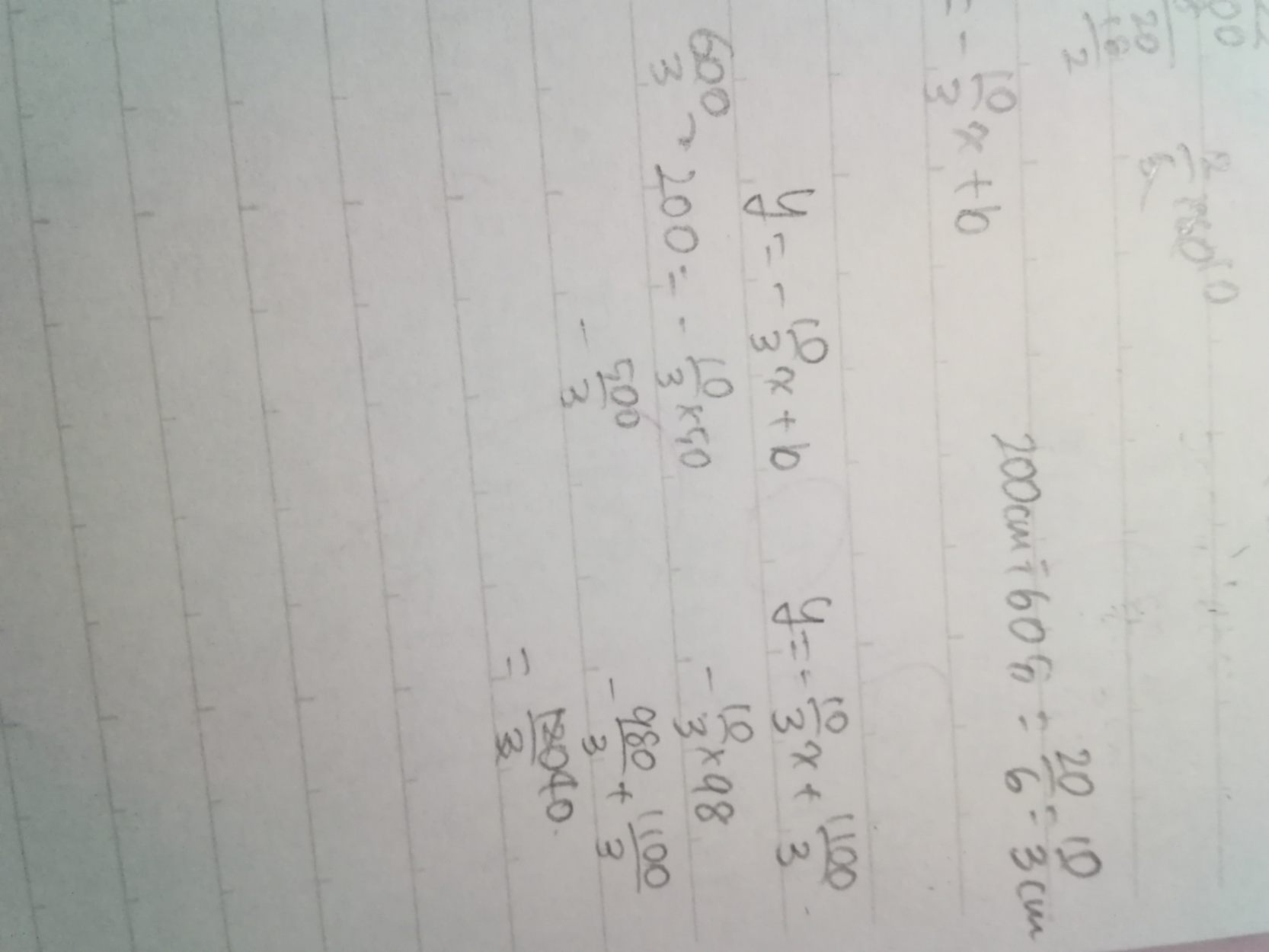
回答
かえでさん、こんばんは。
え?私も答は40cmになりましたが違うのですか?
排水時のxとyの関係式はあなたと同じなんです。
1次関数の式を使わなくても比例式で高さが減った分が160と求まるので、答は40cmのような気がしますが。
答はいくつなのですか?とりあえずそれを教えてください。
==================
解き直しました。もっとうまい方法もありそうですが、とりあえず、答はたしかに68cmです!
高さが80cmになるまでの「1分当たりの高さの減る量」をaとします。
高さが80cmになるまでには $\dfrac{120}{a}$ 分かかります。…①
高さが80cmから40cmまでは、それまでの底面積が2/3になるので、「1分当たりの高さの減る量」は前の3/2倍になり、毎分$\dfrac{3}{2}a$ cmです。この部分で高さが80から40になるので40cm減るのには $40\div \dfrac{3}{2}a=\dfrac{80}{3a}$ 分かかります。…②
そのあと高さが40cmから0cmになるまでは、底面積がその前の1/2になるので「1分当たりの高さの減る量」は前の2倍すなわち毎分3acmとなり、高さが40cmから0cmになるまでは $\dfrac{40}{3a}$ 分かかります。…③
①②③の合計が60分なので、
$\dfrac{120}{a}+\dfrac{80}{3a}+\dfrac{40}{3a}=60$
というaについての方程式が得られます。分母にaがあるのはいやなので、全体にaをかけて1次方程式にして解くとaの値が求まります。やってみてください。そのaの値をもとに①は45分が分かるので、あと3分間でどれだけ減るのか計算すれば、48分後に残った高さが求まりますよ。
これでやってみてください。
ちょっと大変なやり方ですが、思いついたのはこの方法です。
どこかの高校入試問題なんですか?
答えは68cmでした
あ、私も間違えていました。排水によって変化する水面の高さは一定ではありませんでしたね。沈んでいる直方体のおかげで最後の方は2段階に変化するのでした。1つの1次関数ではダメですね。ちょっと計算しなおします。あなたもやり直してみてください。
いちおう解きましたので上の回答に追記しました。しかし、中学生に解かせる方法としてはどうかなとも思います。解答解説は持っていないのですか?
解いてみたら私も68cmにできました! 富山県の高校入試の過去問です。富山県の数学の入試が1番難しいって聞いたので解いてみたら撃沈です…笑 インターネットに載ってるものなので解説まではありません😭 丁寧な解説ありがとうございました(。•̀ᴗ-)✧
あ、できましたか!それならよかったです😊 県立高校の入試ですか。なかなかな問題ですね。
ほんとに難しいです…笑 解説ありがとうございました~❗️
どういたしまして。あ、明けましておめでとうございます。いよいよですね。がんばってください。
頑張ります❗️