このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
相似
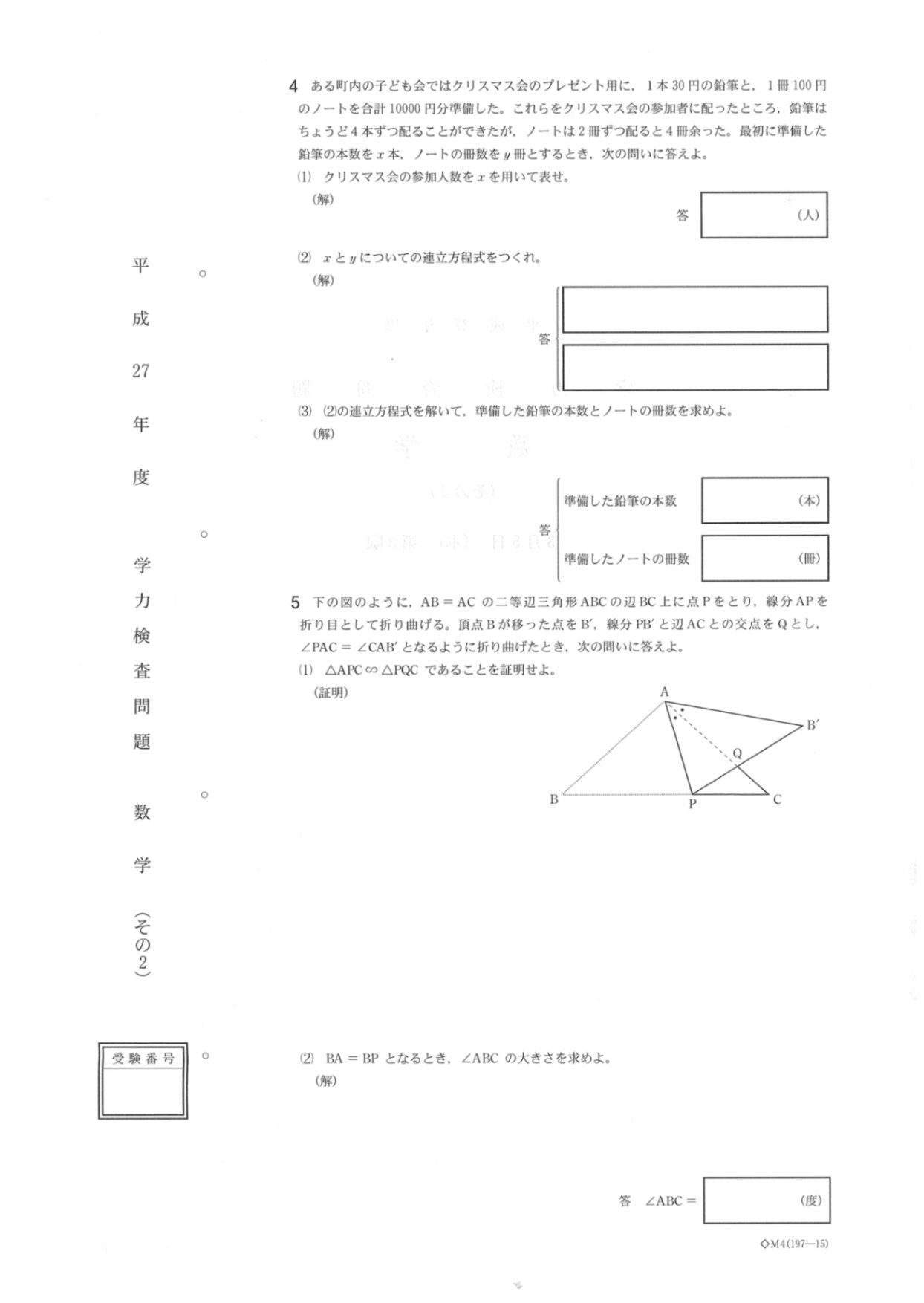
相似問題の(2)がどう考えればいいのかわかりません😭
△ABP≡△PB’Aであってどちらも二等辺三角形ではあるとわかりました❗️
回答
かえでさん、こんにちは。
求める角の大きさをx、∠BACの大きさをyとして、連立方程式を作りますよ。三角形の内角の和=180°というのを二つ作ります。どの三角形か見つけましょう。うまくいかないようならコメント欄に書いてください。
これで大丈夫かな?
△ABC 2x+y=180は分かったんですが、もう一つがどれか分かりません △APB'ではないですよね?
△ABPです! BA=BPですから… また、∠BAP=2/3yになるのは大丈夫ですか? これでできますか?
解答とは一緒になったんですけど、∠BAP=2/3yになるのはなぜでしょうか? ACは折り目の位置に変わらず∠B'APの二等分線になるのですか?
いえ、そうではないです。 ∠B'APは∠BAPを折り曲げただけですから大きさは同じです。ですから∠BAPも・が2つ分の角です。 結局∠BAB'は・4つ分。∠BACは・3つ分。∠BAPは・3つ分になりますよ。よって∠BAP=yは∠BACの2/3になります。 これで大丈夫ですか?
なるほど! 分かりました!ありがとうございます✴️
それならよかったです😊またどうぞ!