このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
三角形の成立条件と外接円の関係について
こんにちは!
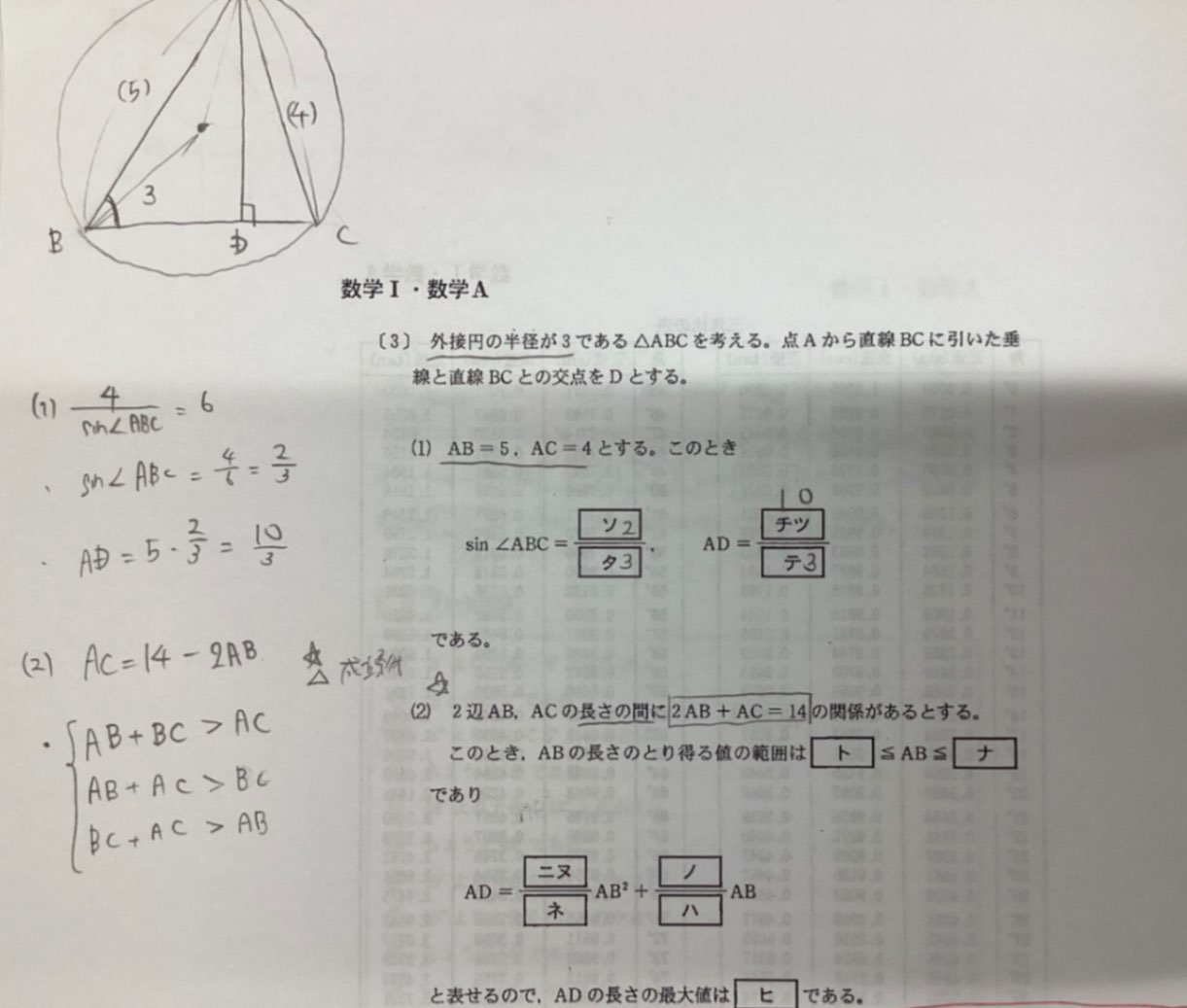
添付画像の問題の(2) ABの取りうる値の範囲を求める穴埋め[ト][ナ]について教えていただきたいです。
・[ト][ナ]の部分では三角形ABCが成立するABの範囲を求めていると考え、私は三角形の成立条件を考えましたが、うまく解けませんでした。
・解答では「0<AB<=外接円の直径」とされており、これが必要条件であることは理解できます。ただ、三角形成立の必要十分条件であるのか疑問です。
【お聞きしたいこと】
三角形が成立する必要十分条件として、0<AB<=外接円の直径 は成り立つのでしょうか。ご教示よろしくお願いします🙇
(問題の理解がずれているのであればそちらも教えていただけると嬉しいです!)
回答
Maru Masa さん、こんにちは。
ちょっと誤解されているようです。辺の長さが直径より大きくなるわけはありません。ABの範囲を言っているだけで、他の辺の長さと関連した問ではないし、三角形の成立条件とは関係ないですね。
これで大丈夫ですか?
くさぼうぼうさん ご回答ありがとうございます!🙇 問題に2AB+AC=14という2辺の関係式がありますが、他の辺の長さと関連した設問ではないのでしょうか…?
はい、それはそうですが、「このとき」と書いてはありますが、ト、ナについては単にABだけの話のようですよ。まぎらわしいですね。
そうなのですね…🤔 それであれば0<AB<=外接円の直径になることで納得できそうです。 ご回答ありがとうございます!
どういたしまして。またどうぞ!