このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
円
(2)がどちらもわかりません
①は半径が6cmということしかわかりません😭
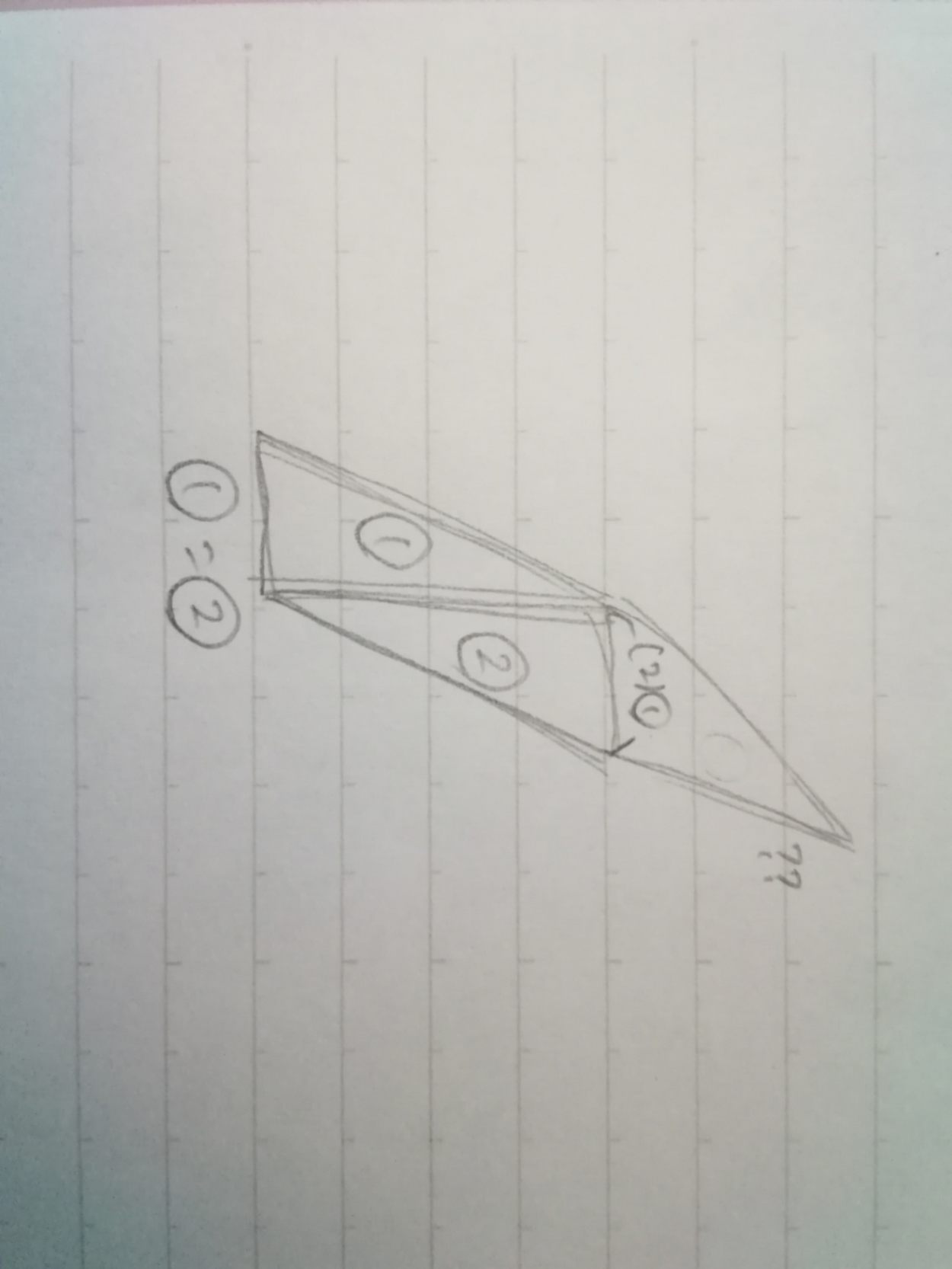
②は写真載せときましたが①の長さを使わないと解けないなと思いました。(上の??はわからないという意味です)
解説お願いします

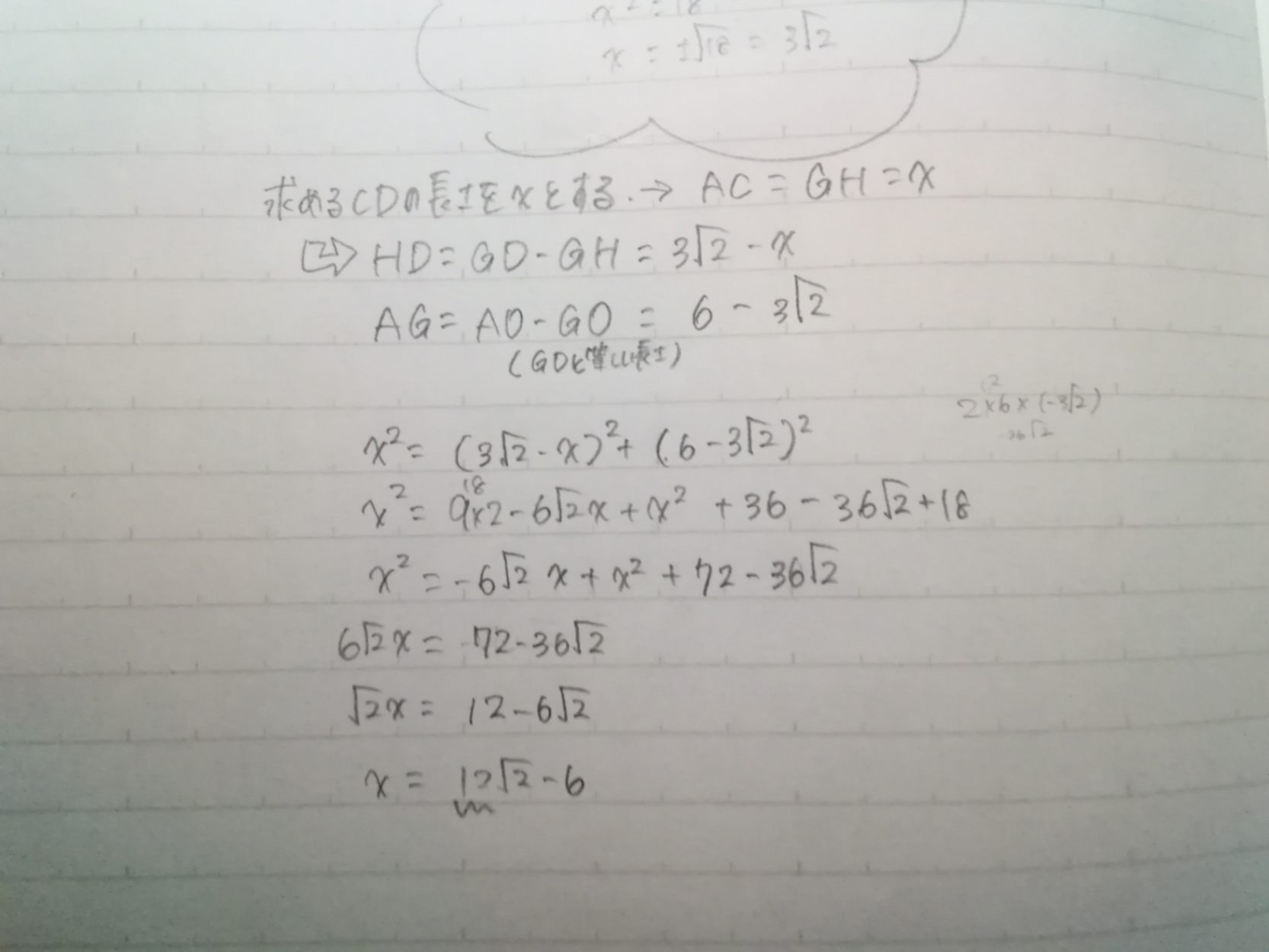
回答
かえでさん、こんにちは。
いやな問題ですね。出題した先生は意地悪な人かも(笑)。
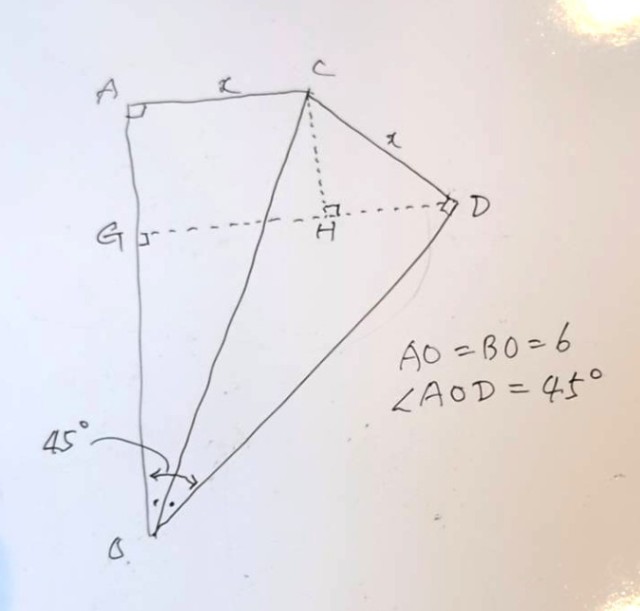
必要な部分だけの図を添付したので、それを見ながら読んでください。
DからAOに垂線DGを引きます。
CからDGに垂線CHを引きます。
弧の長さの関係から∠AOD=45°がわかります。大丈夫?
△GODは直角2等辺三角形になるから、OD:DG=1:√2。
つまり6:DG=1:√2。これよりDG=3√2。
求めるCDの長さをxとするとACもxですよ(分かりますか?)
よってGHもxとなり、HD=3√2ーx…①
OG=DG=3√2で、AO=6だから
AG=6ー3√2
これはCHと同じで、CH=6ー3√2…②
直角三角形CHDに①②とCD=xを当てはめればxの方程式のでっきあっがり~!
これを展開して整理すればxすなわちCDの長さがわかるのです。
やってみてください。うまくいかないようなら言ってください。
正解は持っていますか?
面積の方は、△OEBと△OBDに分けてそれぞれ求めて足せばいいです。
EB=AC=CDですから。
また△OBDの方は、底辺をOBと見て、高さはGDですよ。
これでやってみてください。結果報告や質問は下のコメント欄に書いてください。
①の最後がうまくいきません💦 どこか計算ミスしてますか? 解答は6√2-6です
あれ!最後の行で間違っています! したから2行目の式を√2で割ったんですよね。 12を√2で割る計算が違っています。慎重に! 分母の有理化ですよ。 これでxは求まるかな?
できました! ご丁寧な説明ほんとにありがとうございます✨✨️ とてもわかりやすかったです^^
お役に立ったのならよかったです!