このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
図形の性質証明
画像載せ忘れててややこしくなってしまいすみませんでした🙇♀️
ご解答ありがとうございました💗
また別の問題になります。
基50
証明問題なのですが、途中でわからなくなりました。これでは証明できてないですよね、、、
基51
一応証明できたつもりなのですが、あまり自信がありません、、（特に中点連結定理の逆を使って良いのか自信ないです）
回答
百花さん、こんにちは。
基５０の（１）は、それではダメですね。
AB+AC>BD+DCから
AB>BDとAC>DCは
導けませんよ。
１＋６＞２＋４から
１＞２と言ったら偽です！
ここは角の2等分線の性質を使っていかないと無理でしょう。
AB:AC=BD:CD ですね。
（外角の2等分線でも成り立ちますよ。AB:AC=BE:CE）
私は最終的にはABーBD>0を示しました。
上の比例式からBDを求め、それをABから引いて、分子をうまく変形し、三角形の成立条件AB+AC>BCが使えるようにしますよ。
やってみてください。うまくいかなかったらどこまでできたかを見せてください。
基５１の証明は、それでいいです。論理的にまったく問題ないですよ。ただ、だいぶ回りくどいですねぇ（笑）。
もうちょっと楽にできます。
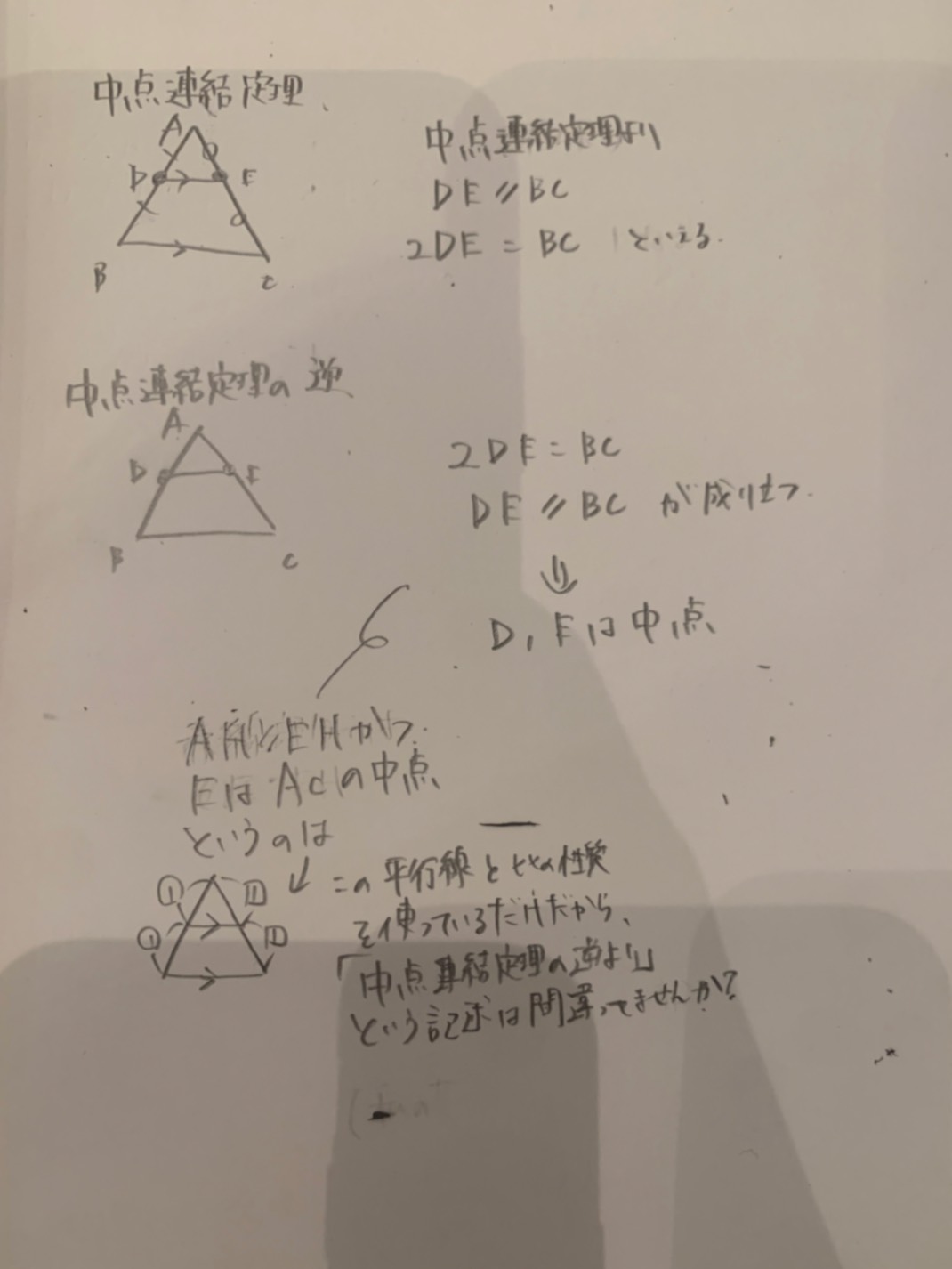
△ADCで、AD//EHかつEはACの中点だから、（中点連結定理の逆より）HはCDの中点です。
AI=IEが分かったあと、△ADI≡△EFIを言えば（あるいは１：１の相似でもいい）DI=FIすなわちIはDFの中点であるといえます。
そんな感じでどうでしょうか？
これで大丈夫ですか？
ありがとうございます！ 解き直してみました！
（1）もやってみました、、できてますかね？
（１）完璧です！！ 4枚目の写真にある中点連結定理の逆の話ですが、 「1つの辺の中点から他の辺に平行な線を引くと、もう一方の辺の中点で交わる」「仮定＝中点、平行 結論＝中点」というのも一般には中点連結定理の逆と言っていますよ。そりゃぁ確かに平行線と比で片付くのだからわざわざ書かず「平行線と比の関係より」だけで済ましてもいいです。どっちを書くのが経済的かなぁ。そんなことを言ったら、そもそも中点連結定理だって単に２：１の相似な三角形を見ているだけなので「相似だから」だっていいのです。ま、「中点連結定理より」とか「中点連結定理の逆より」って書いたほうが余計なことを果敢く手もいいですし全体がすっきりします。 中点連結定理は仮定が２つ、結論が２つなので、逆といってもいろいろあるのです。厳密には逆ではないものもありますよね。