このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。

方程式の解き方

    只隈 佑汰 (id: 4481) （2026年1月16日23:04）
    0 0
    sin x +2x=0 と 2π=2x+sinx の解き方を教えてください

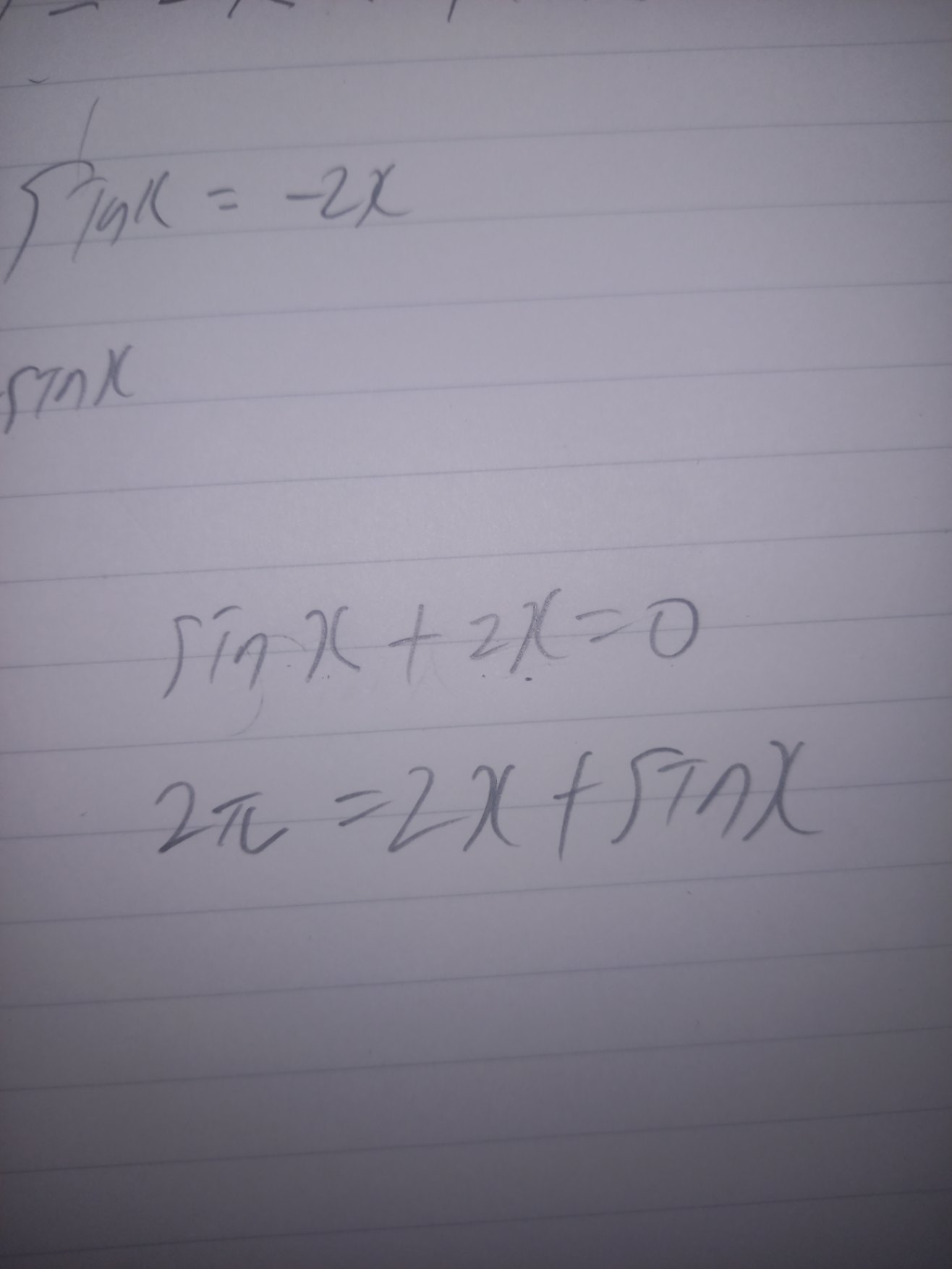
    20260116_230423.jpg

    回答

    くさぼうぼう : (id: 1236) （2026年1月16日23:22）
    0 0
    前のと同じように ｙ＝－２ｘのグラフとｙ＝ｓｉｎｘのグラフとの共有点はグラフから明らかになりますが。 ｙ＝－２ｘ＋２πのグラフとｙ＝ｓｉｎｘのグラフとの共有点もグラフから…ちょっと明らかじゃないか。この場合はｙ＝ｓｉｎｘを微分してｘ＝πでの接線の傾きと直線の傾きー２を比較して、グラフから共有点が読み取れますよ。 これじゃダメなの？ このような方程式は自明な解としては分かりますが、残念ながら高校数学で厳密に解くことは無理なんです。 これでどうでしょうか？
    回答する