このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
大小比較
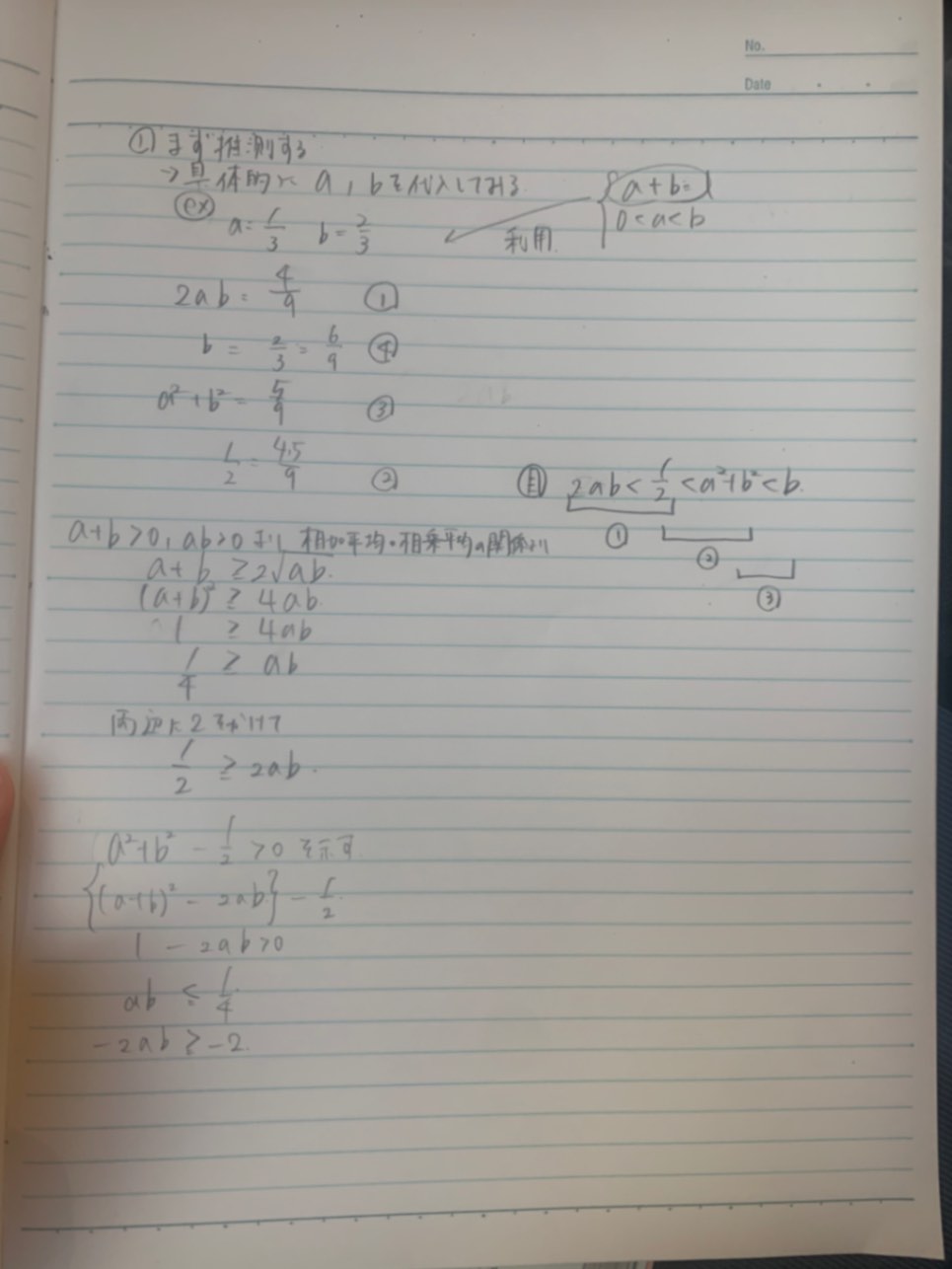

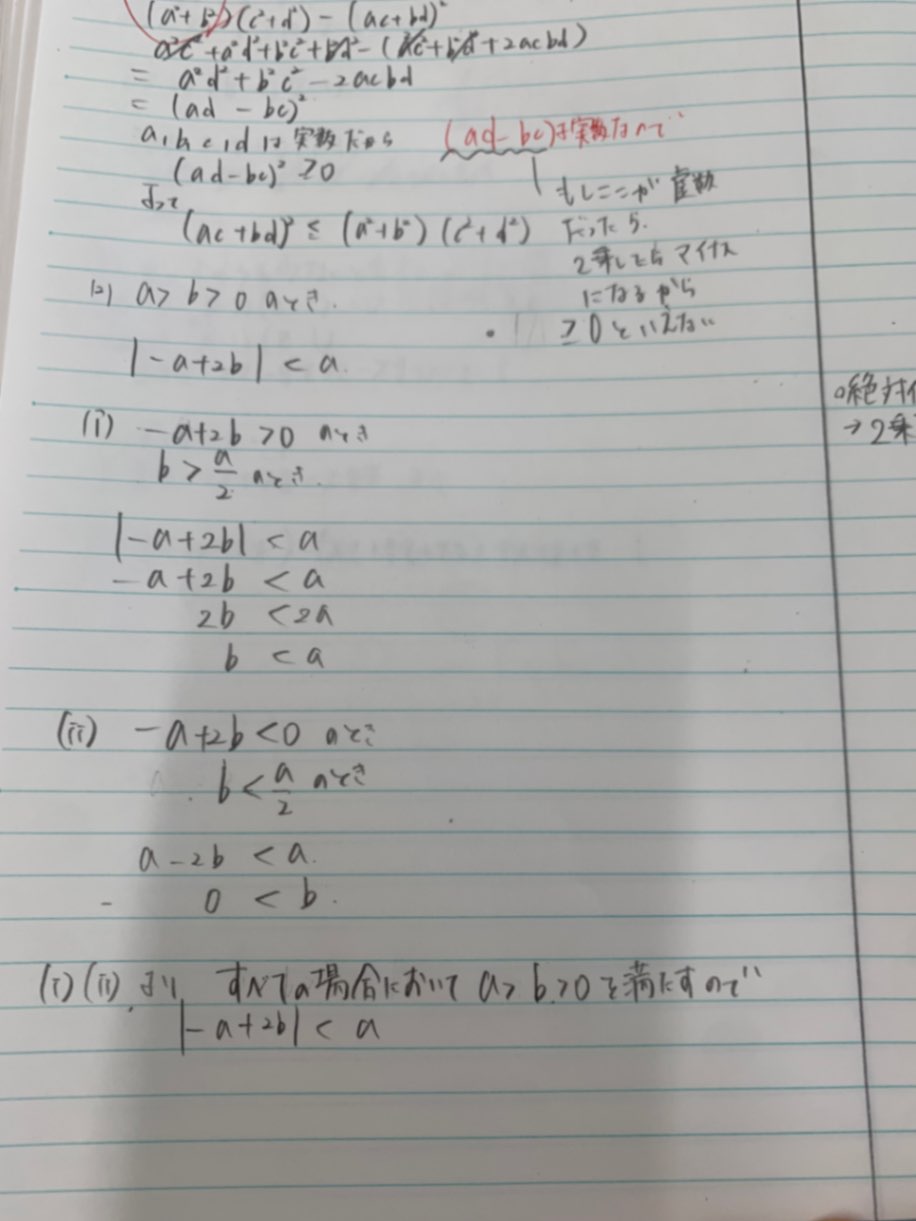

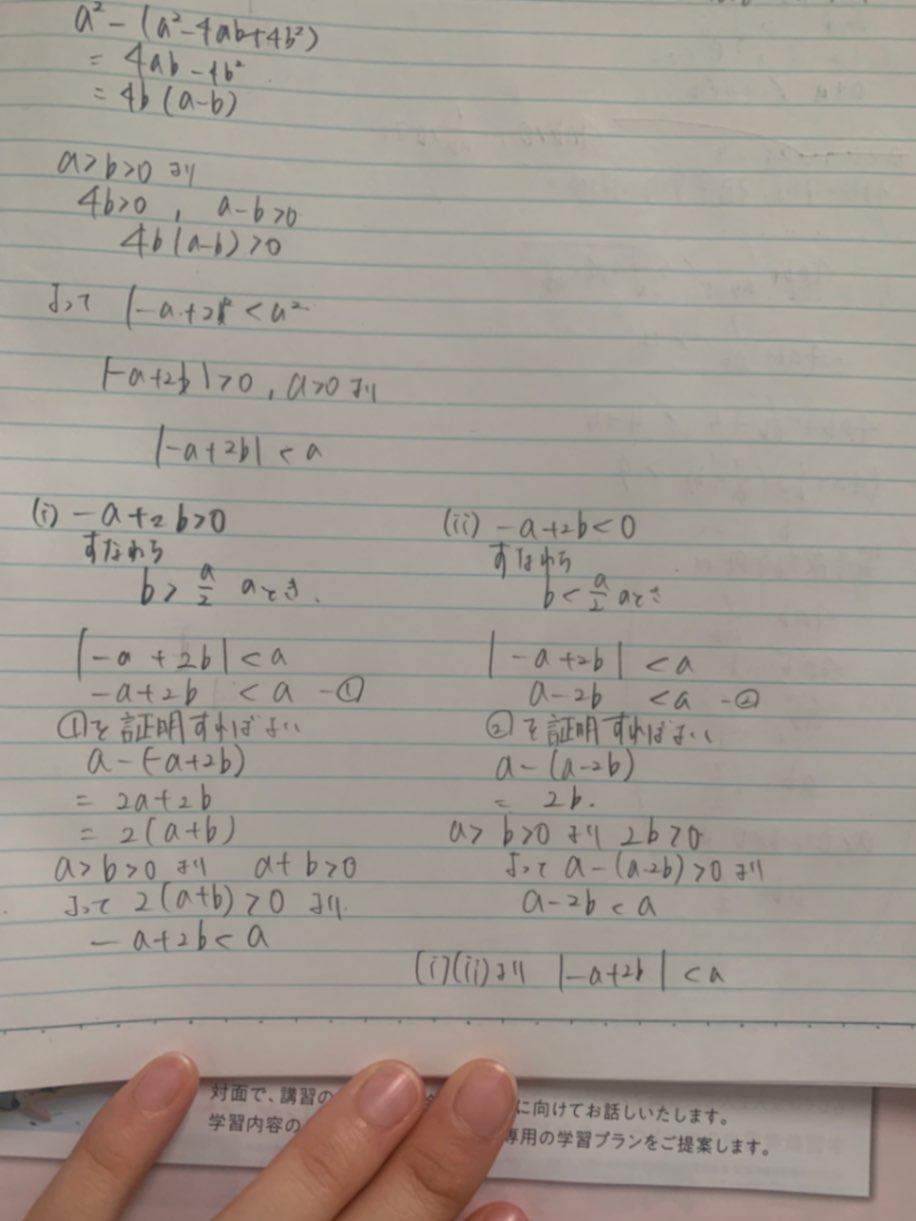

回答
聞き方が悪くてすみません🙏 29も教えて欲しいです 1番目の写真は 29を解いている途中です💦
28の( 2)についてです 場合分けして解いてみたのですが合ってますか?
場合分けして解いたやつ間違えてる気がします💦 でも、どこがダメなのかはいまいちわからないでいます、、
上の回答に追記しました。読んでください。
ありがとうございます🙏 やってみました。
4枚目の写真、②の不等式の証明は完璧です!でもその下、たぶん③の証明だと思うのですが、下の方の2列のなって書かれている右側の「2ab<1/2より」の次の式はおかしいですね。右辺はー1/2では?もうちょっと考えてください。 5枚目の写真、2乗して比較する方法の証明は大丈夫です!そこで証明は終わっているんですよね。その下の(i)(ii)は、場合分けでやる方の証明ですね。(i)か(ii)のどちらかに等号の入った不等号を使わないと=の場合が抜けてしまいますので注意。(i)のほうの「①を証明すればいい」の次の次の行は間違ってます。(ii)のほうはOKです! これでわかりますか?
4枚目の写真、②の不等式の証明は完璧です!でもその下、たぶん③の証明だと思うのですが、下の方の2列のなって書かれている右側の「2ab<1/2より」の次の式おかしいですね →考えてみたんですけど、何がダメなのかわからないです😭 確かに自分でも間違えてるなというふうには感じます、、 教えてください🙏
「何がダメなのかわからないです😭」と言われて私もあなたの意図をもう一度よく考えました。 私ははじめは2ab<1/2という不等式の左辺にー1を足しているので右辺にも足してー1/2としなければいけないと思っていたのですが、 1/2>2ab>2ab-1という意味で考えて途中を抜いて1/2>2ab-1と書いたのか!と気が付きました。すみません、あなたのままで大丈夫です。失礼いたしました😭
あ、証明の方は大丈夫、正しくなりました!
ありがとうございます🙇♀️