このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
画像の問題セについて
度々申し訳ありません。
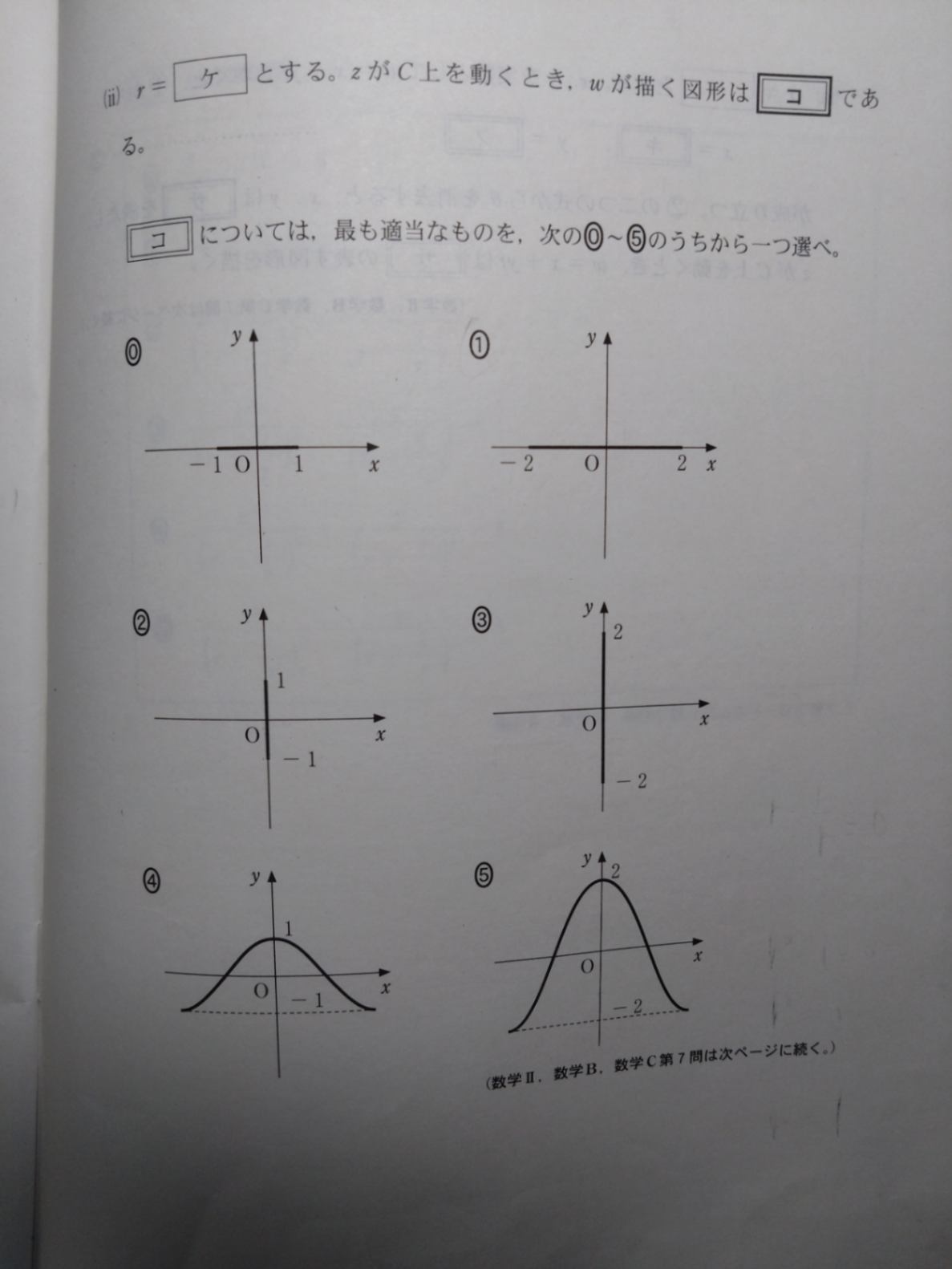
解説の記載の中に、「w^2=z^2+1/z^2+2から、w^2が動く図形は、点2を中心として長軸が実軸に平行な楕円」とあるのですが、点2を中心としているとこの式からの導き出し方を教えて頂けないでしょうか。
よろしくお願い致します。



回答
hana はな さん、こんにちは。
画像が5つまでなのですね。道理で抜けているようでした。でも大丈夫です。
複素数$z^2+\dfrac{1}{z^2}$ が楕円であることはいいのですね。
それなら。その複素数に2を足すということは、その複素数を右に2だけ動かすことですよ。
楕円上のすべての点に2が足されますから、形は同じ楕円のまま、中心も2だけずれて、0だったものが2になる、ということです。
これでわかりますか?下のコメント欄になにか返事を書いてください。よろしく。
いつも回答ありがとうございます。 複素数に足した場合の移動については理解しました。 ですが、よく考えてみたらなぜz^2+1/z^2が楕円になるのか理解していませんでした。 z^2が原点を中心として半径r^2の演習を動くとなぜ楕円になるのしょうか。 お手数おかけして申し訳ありません。
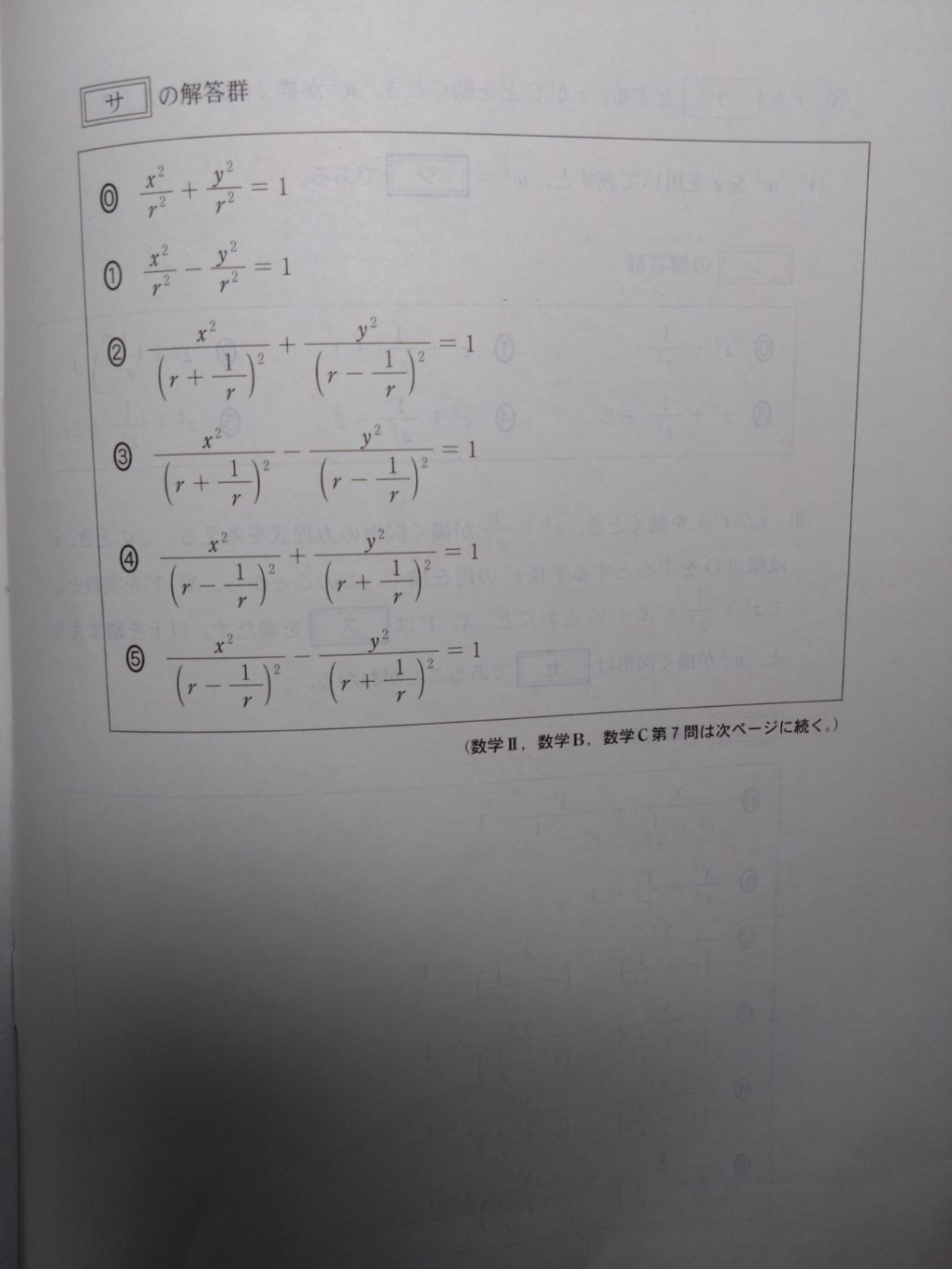
あはは、そうでしたか。それは(問題が見えないけど)たぶんサのところで楕円が示されていますね。サの答のrの代わりにr²を使ったのがスの答です。だからこれも楕円ですよ。で、w²はそれに2を足すかっこうになっています。2は(z+1/z)²の展開から出てきてますね。 これで大丈夫ですか?もしサがわからないのなら、そう言ってくださいね。
画像を差し替えました。 サシまでは分かるのですが、スでサの答えをr^2にすれば良いとどうやったら判断できるのでしょうか。 z+1/zがz^2+1/z^2になっているからなんでしょうか。
そうです!形式が同じで2乗があるかないかだけなので、まえの変形の式のrの代わりにr²を使えます。 サの部分、ありがとうございます。わかりました。 これで大丈夫ですか?
あ、角はθではなく2θになりますが、それはθ’とでも考えれば、式の変形はまったくおなじになります。
納得しました。 ありがとうございます。 またお願い致します!
それならよかったです!またどうぞ。
画像を載せられるのが5つまでなので、全てを載せることができませんでした。すみません。