このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
絶対値の計算
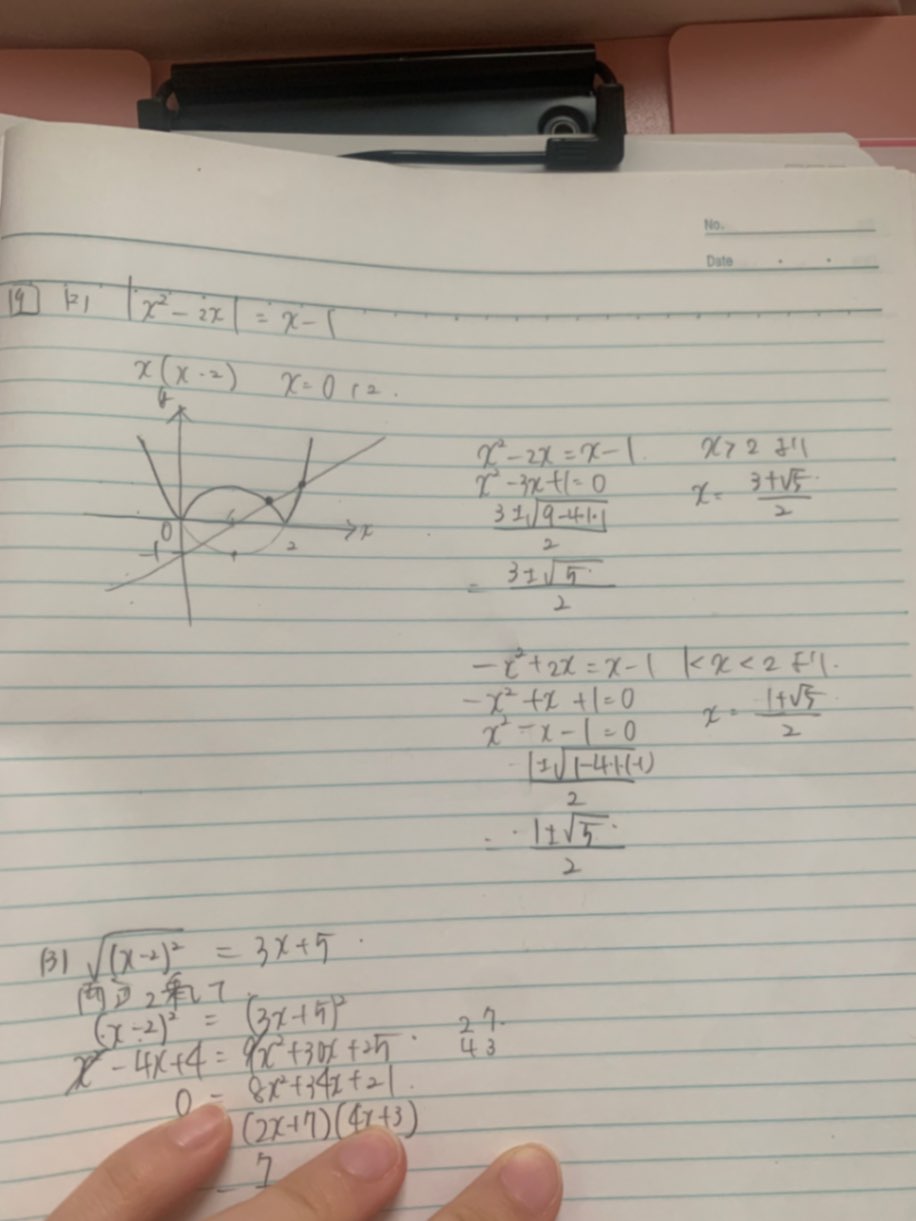
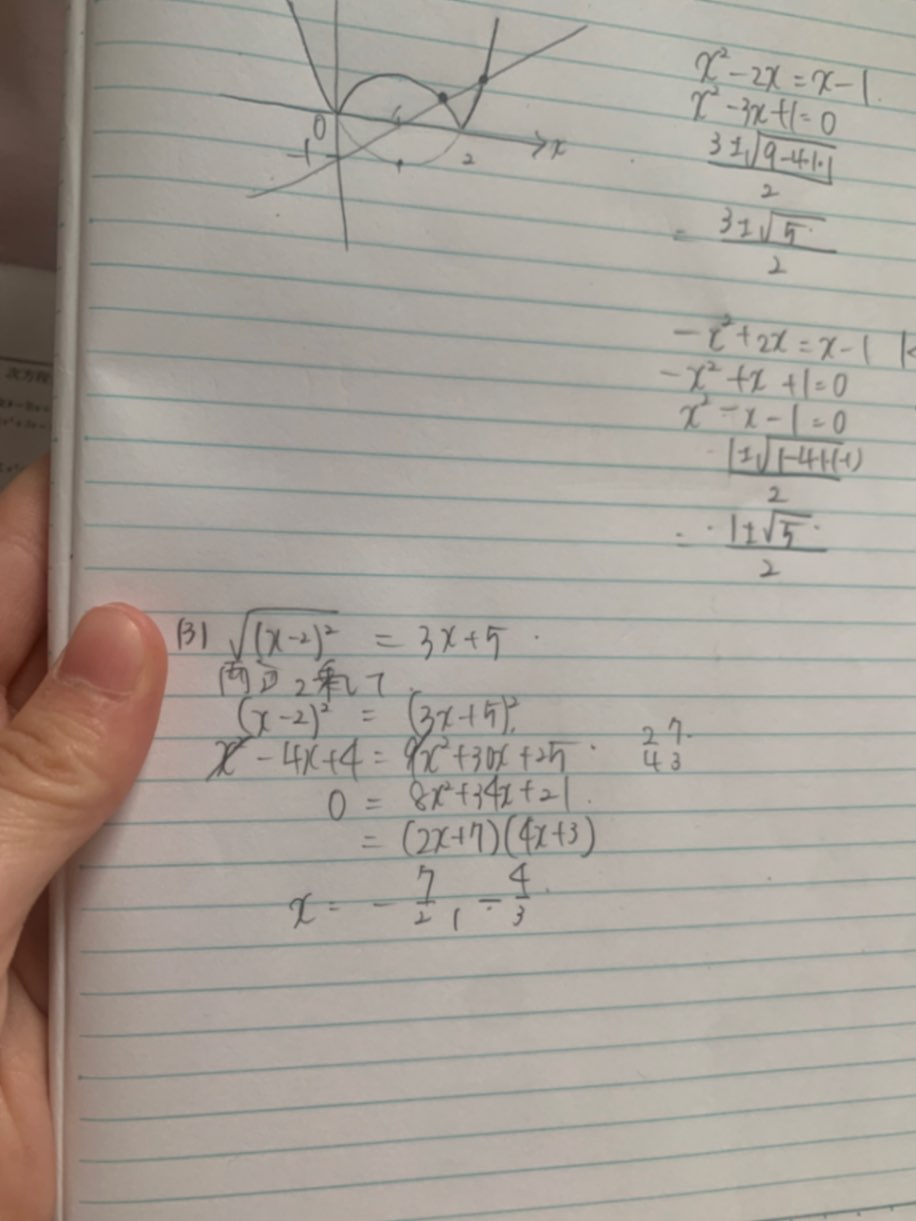


回答
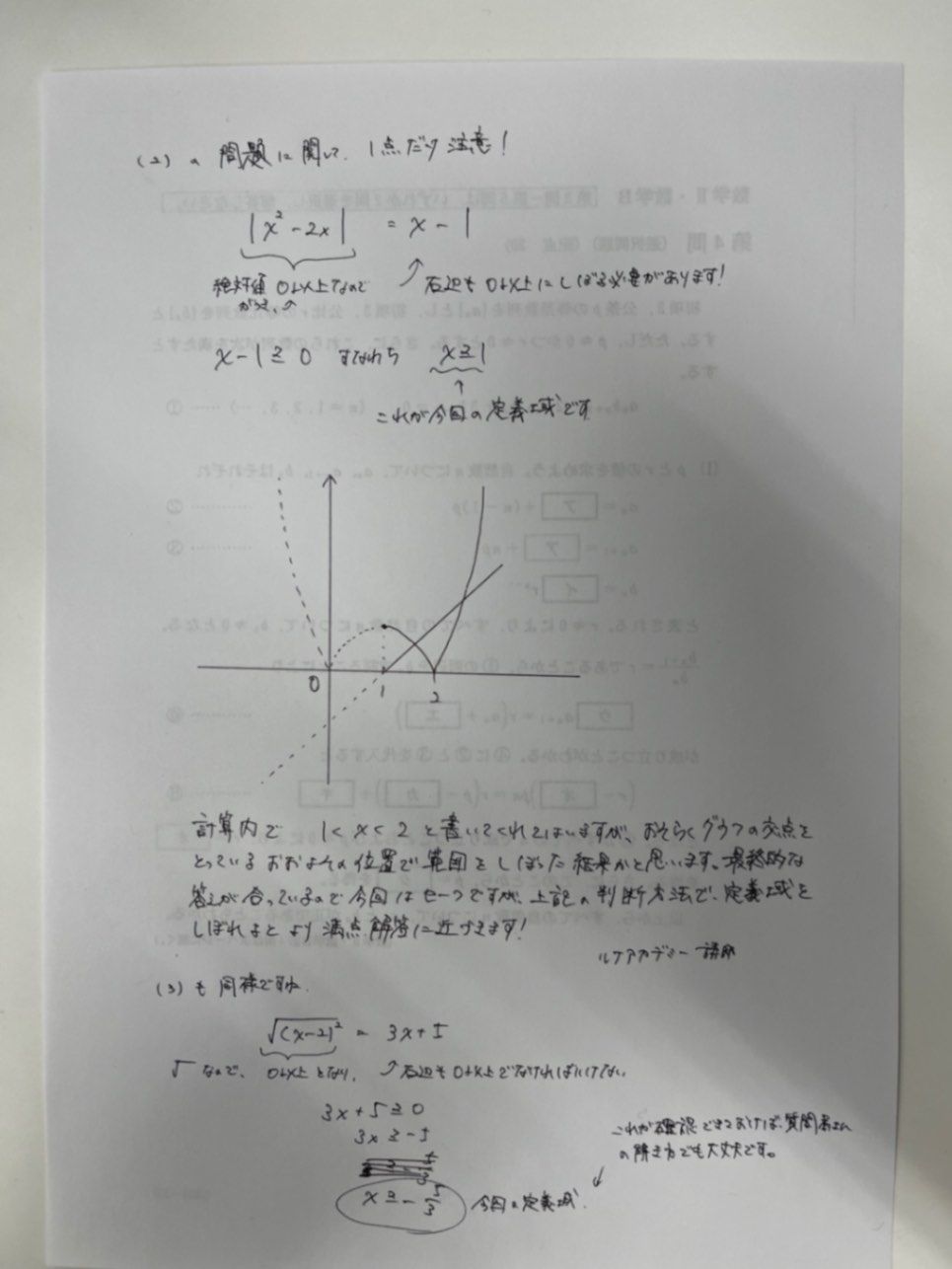
剛志さん、悪意でいちゃもんを付けているのでは絶対にありません。百花さんが混乱しないように書いています。誤解しないで下さいね。関数でもないのに定義域はおかしくないかとおもうのですが。方程式ですから、その方程式を成り立たせる数を見つけるだけのことでは?強いて言えば「(2)ではもし解が存在するならば、解は1以上であることが分かっている」くらいではないでしょうか?方程式でなく、不等式になったら、右辺が負であっても可能ですし、生徒さんにとってはまぎらわしいのでは?
(2)を百花さんは、2つの関数のグラフの交点を求めるやり方なので、グラフもすべての範囲で書くべきだと思うのですが。その全体の中で交点を見つけます。
くさぼうぼうさん、ご指摘ありがとうございます。ご指摘の通り、確かに定義域という言い方はそぐわないかもと思いました。 訂正します。Xの取り得る範囲と言い直します。 Xの取り得る範囲に関しては、確認すべきだという意見に関してはそのままです。「解は、1以上であることが分かっている」のであれば、回答のミスを防ぐためにも書くべきではないかと思いますし、そもそもその範囲に気づいていない場合、条件外の答えも答えてしまいかねないので、確認する方がいいのではないかと考えます。 減点の余地がない回答を目指すのであれば必須かと思います。 また、自分は方程式の話として解説をしてますので、不等式のことに関しては別であると自分自身把握しておりますし、言及しておりません。質問者さんの混乱を招かないためにも質問内容にのみ解説を行なっています。
お説、了解しました。ところで、この質問箱は解答者が少なく、ほぼ私一人で回っています。私はこのサイトの制作者でもなく単なるボランティア回答者です。月川様もぜひここの回答者としてご参加ください。1つの質問に回答が複数付くのはかまいません。ぜひよろしくお願いします。私はもう後期高齢者で、夜は早く、10時以降の質問の回答が翌日になってしまいます。その時間帯あたりもご協力いただけたらと思います。どうぞよろしくお願いします。
ありがとうございます🙇♀️ ルートは「2乗して中身になる0以上の数」と定義されているから場合分けしないなら、絶対値をつけないと外せないんですね!
場合分けしないときはX取り得る範囲に注意しないといけないんですね💦