このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
極形式
青ペンの部分の変形はどのようにして思いつきますか?
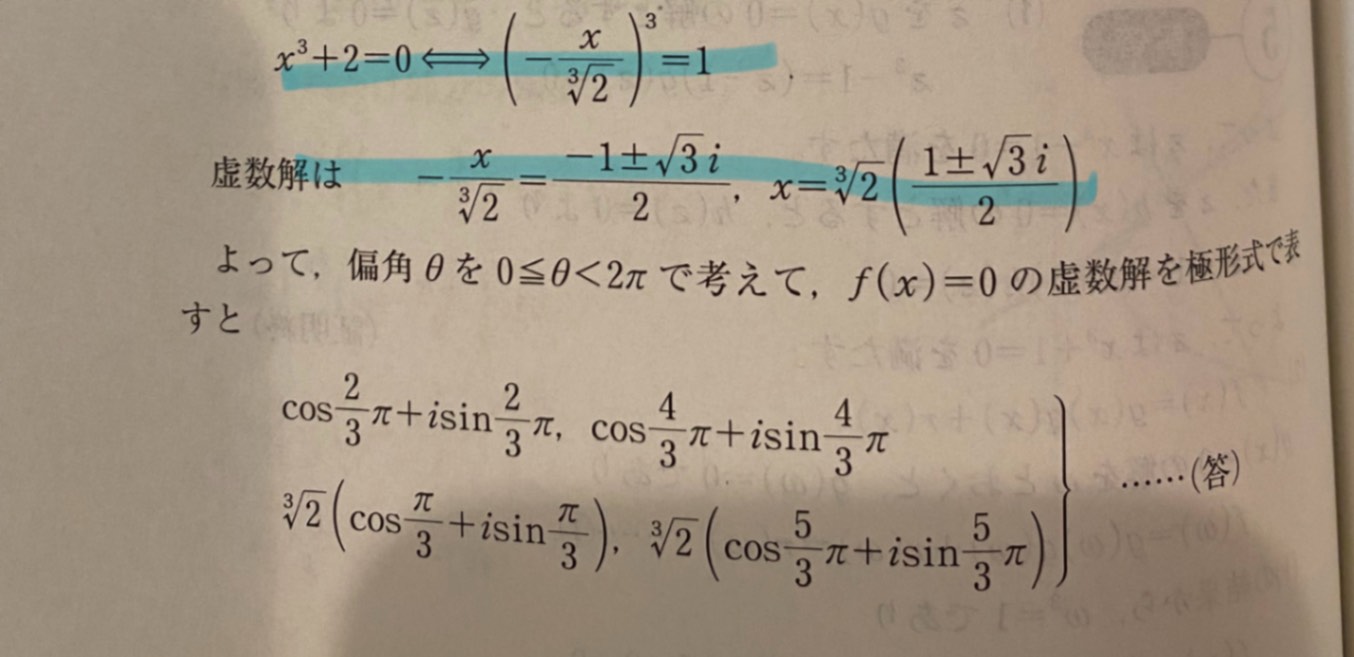
回答
$x^3+2=0$
$x^3=-2$
$\frac{x^3}{2}=-1$
$-\frac{x^3}{2}=1$
$\left(-\frac{x}{\sqrt[3]{2}}\right)^3=1$
以上が一行目です。
そして、$A^3=1$の実数解は$A=1$で、虚数解は$A=\frac{1±\sqrt{3}}{2}$なんです。
今回Aの部分が$\left(-\frac{x}{\sqrt[3]{2}}\right)^3$なんですね。ただ、Aの部分がマイナスなので、$A=\frac{1±\sqrt{3}}{2}$にマイナスがついて$A=\frac{-1±\sqrt{3}}{2}$となっています。
即ち、$\left(-\frac{x}{\sqrt[3]{2}}\right)=\frac{-1±\sqrt{3}}{2}$
これを$x$について整理する。
分からなかったらコメントしてください。
Keitaさんの回答で一部間違いがあります。
虚数解は $A=\dfrac{-1\pm \sqrt{3}i}{2}$ です。先頭のマイナスと虚数単位iが抜けてます。
$\left(-\dfrac{x}{\sqrt[3]{2}}\right)^3=1$ より
$A=-\dfrac{x}{\sqrt[3]{2}}=\dfrac{-1\pm \sqrt{3}i}{2}$
よって
$x=-\sqrt[3]{2}\cdot \dfrac{-1\pm \sqrt{3}i}{2}$
$=\sqrt[3]{2}\cdot \dfrac{1\mp \sqrt{3}i}{2}$
$=\sqrt[3]{2}\cdot \dfrac{1\pm \sqrt{3}i}{2}$
$=\sqrt[3]{2} \left( \dfrac{1\pm \sqrt{3}i}{2}\right)$
となりました。マイナスプラスが1カ所しかないので、それはプラスマイナスにすることができますよ。
これで大丈夫ですか?
すいません(☉。☉)! 訂正ありがとうございます
理解できました。お二方ともありがとうございます。
どういたしまして!またどうぞ。