このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
間違っている点を教えてください!
自分の解き方ではどこが間違いなのでしょうか
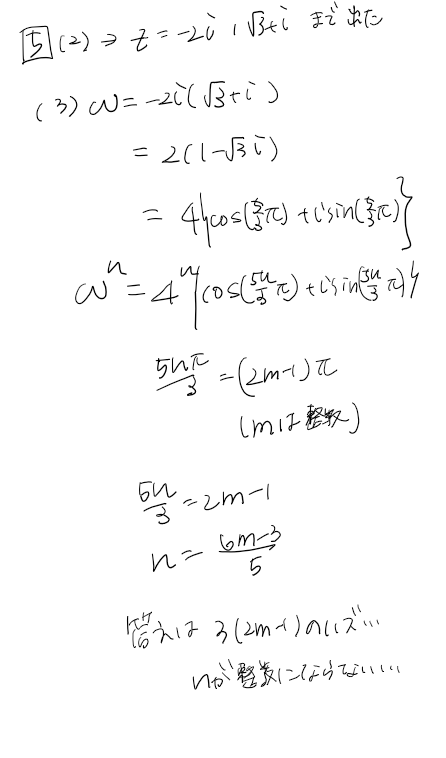

回答
まかろん さん、こんばんは。
いやいや、間違っているわけではないですよ。
まだ途中だということです。
あなたが得た $n=\dfrac{6m-3}{5}$ は、とりあえず「$\omega ^n$ が負の実数になるような『実数』nの条件」までです。
問題の整数nにとってはまだ必要条件です。
まだnが整数であるという条件は求まっていませんよ。
「$n=\dfrac{6m-3}{5}$ が整数になるためには…」という議論が続きます。
$n=\dfrac{3(2m-1)}{5}$ が整数であるためには、分子が約数5を持つときである。
5と3は互いに素なので、$2m-1$ が奇数の5の倍数であればよい。
$2m-1=5(2k-1)$ (kは整数)と書けるはず。
……
この先、やってみてください。nの条件がkの式として出てきます。
これで大丈夫ですか?
結果報告をお待ちしています。
うまくいかないときは、下のコメント欄か写真かでさらに聞いてください。