このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
数列の極限
こんばんは!
問題文に書かれている分子のnが、解説で1と書かれていることが疑問点です。
私は、n^2で割って1/nになるのではないかと考えていました。
解答よろしくお願いいたします。
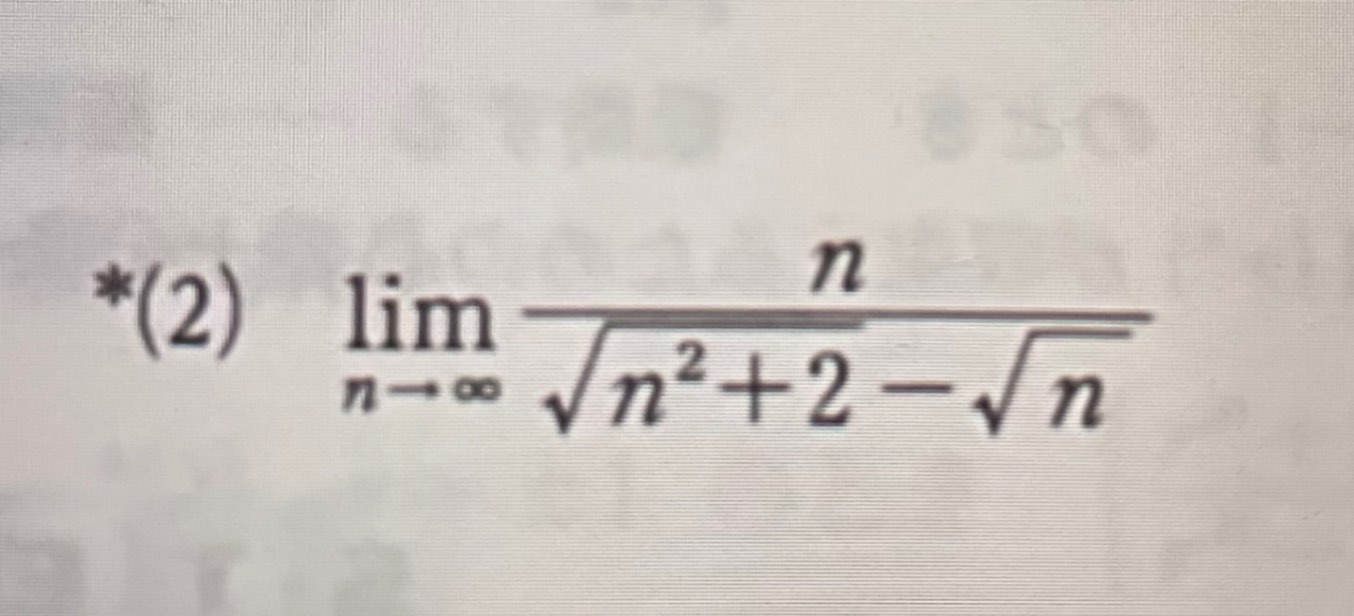
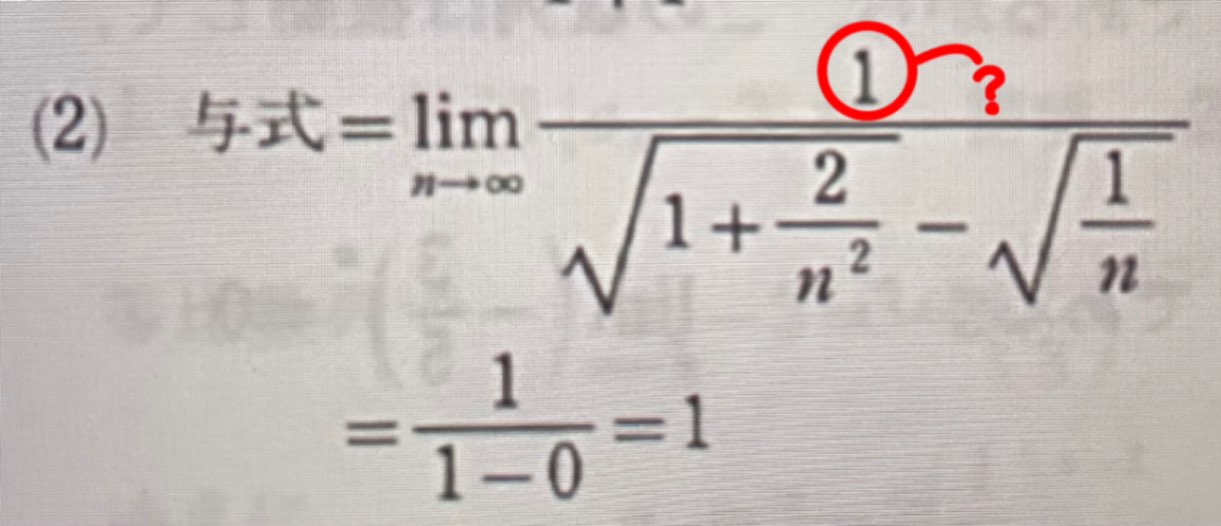
回答
Chi さん、こんばんは。はじめてのかたですね。よろしく。
その計算は、分母分子をn²ではなくnで割っているだけです!
ルート記号の中の入るとn²で割ることになりますよ。
$\sqrt{n^2+2}$ を 正の数$n$ で割ると
$\dfrac{\sqrt{n^2+2}}{n}$
$=\dfrac{\sqrt{n^2+2}}{\sqrt{n^2}}$
$=\sqrt{\dfrac{n^2+2}{n^2}}$
$=\sqrt{1+\dfrac{2}{n^2}}$
また $\sqrt{n}$ を正の数$n$ で割ると
$\dfrac{\sqrt{n}}{n}$
$=\dfrac{\sqrt{n}}{\sqrt{n^2}}$
$=\sqrt{\dfrac{n}{n^2}}$
$=\sqrt{\dfrac{1}{n}}$
もちろん分子は1ですね。
これで大丈夫ですか?
√aを正の数bで割ると $\sqrt{\dfrac{a}{b^2}}$ になることは、しっかり理解して使えるようにした方がいいです、というか、しないとこれからの極限の学習で行き詰る可能性が高いです。
ここでは会話型を目指しています。
これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、下のコメント欄になにか返事を書いてください。返事がないと、せっかく書いたものを読んでくれたのかどうか、書いたものが役に立ったのかどうか、こちらではわからないのです。コメントよろしく。
よく分かりました!ありがとうございます。 今後ともよろしくお願いします!
あ、今しがた上の回答にちょこっと追加しました。√aのとこです。読んでおいてくださいね。 お役に立ったのならよかったです。 またどうぞ!!